Inducción electromagnética. Ecuaciones de Maxwell

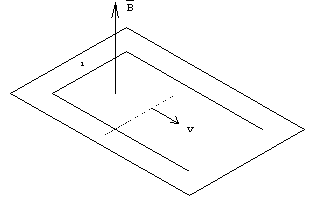
1.-Se coloca un circuito plano de N vueltas, cada una de área S, perpendicularmente a un campo magnético uniforme que varía con el tiempo de la forma B=B₀ sen(wt).

• Calcular la f.e.m. inducida.
• Representar el campo magnético y la f.e.m en función del tiempo.
• Representar en el circuito el sentido del campo y de la corriente inducida en cada cuarto de periodo.

2.-Calcular la f.e.m. inducida en el circuito de la figura. Indicar el sentido de la corriente inducida. Datos: l=0.5 m, B= 0.5 T (apuntando perpendicularmente al papel y hacia dentro), v=4 m/s.

3.-Una bobina rectangular de N vueltas gira con frecuencia angular w, en un campo magnético uniforme perpendicular al plano del papel.

Hallar la f.e.m. inducida.

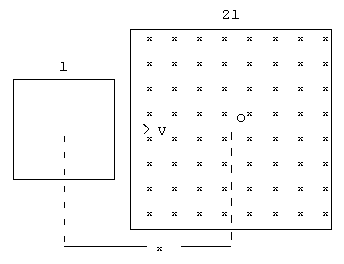4.-Una espira cuadrada de alambre se mueve con velocidad v constante en dirección transversal a un campo magnético uniforme confinado en una región cuadrada cuyos lados son de longitud doble que los de la espira. Calcular el valor de la f.e.m. y dibujar el sentido de la corriente inducida en las siguientes situaciones: La espira se está introduciendo en la región. La espira está en la región. Está saliendo de la región. Ya ha salido de la región en la que existe el campo magnético.

5.-Hallar el coeficiente de autoinducción de un solenoide muy largo de longitud L, de N espiras y de sección S.

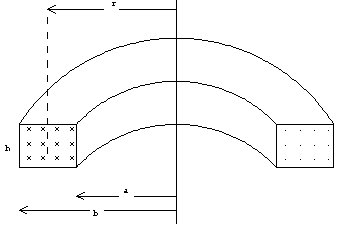6.-Calcula el coeficiente de autoinducción del toroide de N espiras y de las dimensiones indicadas. Datos: a=5 cm, b=10 cm, h=1 cm, N=1000 espiras

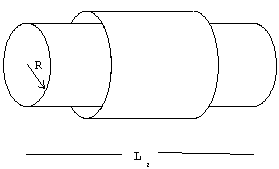7.-En la figura se representan dos solenoides rectos, largos y concéntricos, de longitudes L1 y L2. Sus números de espiras son N1 y N2, y las intensidades de las corrientes que los recorren I1 y I2 .Las secciones de ambos son círculos siendo R el radio del solenoide interior. Hallar el coeficiente de inducción mutua Demostrar que M12=M21.

8.-Para convertir el voltaje de 220 V de un enchufe a un voltaje de 9 V de una radio utilizamos un transformador. Si el primario tiene 440 vueltas.

• ¿Cuántas debe tener el secundario?
• Calcular la corriente que debe pasar por el primario si la radio funciona con 360 mA.

9.-En un circuito formado por una resistencia y una autoinducción en serie, se le conecta una batería

• Calcular la corriente para t=1 s.
• ¿A qué valor tiende asintóticamente la corriente?.

Datos: V₀=12 V, R=25 W, L=0.48 H.

10.-Obtener a partir de la ecuación de un circuito LC la frecuencia de sus oscilaciones libres. En un circuito LC la autoinducción vale 5.3 mH, y la capacidad 17 nF, la carga inicial del condensador es de 2.2 mC, la corriente inicial es nula.

• Escribir las expresiones de la carga en el condensador, y de la intensidad en la autoinducción en función del tiempo.
• La ecuación de la energía asociada al campo eléctrico en el condensador en función del tiempo.
• Y de la energía asociada al campo magnético en la autoinducción en función del tiempo.
• Comprobar que la energía total es independiente del tiempo.

11.-El campo eléctrico de una onda electromagnética plana es E_x =0, E_y=0.4 sen2p/3(x-ct), Ez=0.3 sen2p/3(x-ct) N/C.

• Determinar la amplitud del campo eléctrico, y del campo magnético de la onda electromagnética.
• Dibujar un esquema en el que se especifique la dirección de vibración del campo eléctrico, del campo magnético y la dirección y sentido de la propagación de la onda electromagnética.
• Hallar la frecuencia, longitud de onda e intensidad de la onda electromagnética.
• Si tal intensidad se mide a una distancia de 3 km de una emisora que emite en todas las direcciones y de forma isótropa, hállese la potencia de la emisora.