Movimiento oscilatorio

1.-El movimiento de un oscilador armónico simple está descrito por la ecuación x=4sen(0.1t+0.5), todas las cantidades expresadas en el S.I. de unidades. Hallar:

• La amplitud, periodo, frecuencia angular, y fase inicial del movimiento
• La velocidad y aceleración en función del tiempo.
• La posición, velocidad y aceleración en el instante t=5 s
• La velocidad y aceleración cuando x=2 m
• El(los) instante(s) en el(los) que el móvil pasa por la posición x=2 m.
• Hacer un gráfico de la posición, velocidad y aceleración en función del tiempo.

2.-Un resorte horizontal tiene una constante recuperadora de 48 N/m. En el extremo del resorte se coloca una masa de 0.75 kg y se estira el resorte 0.2 m a partir de la posición de equilibrio, soltándose a continuación, momento en el que se empieza a contar el tiempo. Hallar:

• El periodo de la oscilación
• La ecuación del M.A.S.
• Los valores de la velocidad, aceleración, energía cinética, potencial y total, del móvil, cuando se encuentra en la posición x=0.1, después de haber pasado por el origen.
• Hacer un gráfico de la energía cinética, potencial y total en función de x.

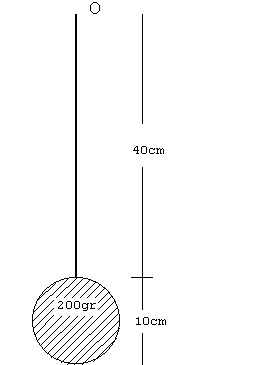3.-El péndulo de un reloj está formado por una varilla de 200 g y 40 cm de longitud y una lenteja en forma cilíndrica de 500 g de masa y 5 cm de radio tal como se indica en la figura. El péndulo puede oscilar en torno a un eje perpendicular que pasa por su extremo O. Si se desvía 10º de la posición de equilibrio, y se suelta, determinar: La velocidad angular de rotación cuando vuelva a pasar por la posición de equilibrio. El periodo de las oscilaciones pequeñas del péndulo compuesto

4.-Un péndulo de torsión consiste en una varilla de masa 100 g, y 30 cm de longitud suspendida de un alambre, perpendicular a la varilla y que pasa por su centro. La varilla a su vez, pasa por el centro de dos esferas iguales de 150 g y 5 cm de radio, situadas simétricamente, de modo que el centro de las esferas dista 10 cm del alambre. Si el periodo de oscilación del péndulo es 2.4 s.

• Calcular la constante de torsión del alambre.

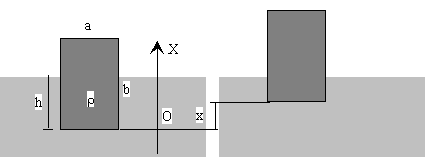5.-Determinar el periodo de las oscilaciones de un corcho en forma de paralepípedo de dimensiones a, b, c. y densidad r, que flota en el agua. Sugerencia (primero hallar la altura h de equilibrio, en segundo lugar hallar la fuerza (módulo y sentido) sobre el corcho cuando se levanta una longitud x).

6.-Encontar la ecuación resultante de la composición de estos dos M.A.S. de la misma dirección y frecuencia

x₁=2sen(wt+p/4) x₂=5sen(wt+p/2)

7.-Componer los siguientes M.A.S. de la misma amplitud A y de direcciones

perpendiculares.

• x=Asen(wt)y=Asen(2wt)
• x=Asen(wt)y=Acos(2wt)