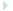Table of Content  Branch Up  

Calculating the Matrix

The size (thus the cost) of the Matrix has proven to be a critical concern. Lets imagine a generic Matrix so we can adjust values until acceptable results are obtained.


These are the variables:

L  : Size of the Linear addressable space.
P  : Size of the PAGE field in the Linear address.
d  : Size of the OFFSET field in the Linear address.
F  : Number of addresses composing a Page Frame in physical memory
E  : Size of a Matrix entry.
A  : Size of the FRAME_ADDRESS field in the Matrix entry.
N  : Number of Matrix entries per Table (that is, per process).
S  : Number of max simultaneous processes.
M  : Total number of Matrix entries (for S processes).

Note: Sizes are in bits.

Here are the relationships between those variables:

d = log2 (F)    ; Number of bits needed to address F
P = L - d       ; A linear address has L bits
A = P           ; This conclusion is easy to obtain
N = 2^P         ; The Trans Table has as many entries as P can address
M = N * S       : The Matrix has as many tables as allowed sim. processes.

We start by fixing the size of the Linear space (L) since that will determine the max amount of physical memory allowed in the system.

Then we fix the size of the page frames (F). Here is a trade-off situation: The smaller is F, the bigger becomes the Matrix; but making F too big will degrade memory management efficiency. We can start with a reasonable value (say, 4KB).

With these two variable fixed, we can start doing the math


#Linear Address fields:

d = log2 (F)   ; Number of bits in the OFF_SET field
P = L - d      ; Number of bits in the PAGE field

#Matrix entry:

A = P          ; Number of bits in the FRAME_ADDRESS field.

The Matrix entry also has control bits (about 4) and can also contain reserved bits. What we do is to add them all, then we round to a multiple of 4 (for practical reasons). Extra bits resulting of rounding will be considered "reserved".

#Trans Table size:

Trans Table is the chunk of Matrix dedicated to one process. The number of entries is:

N = 2^P

So far we have a Matrix that is N rows by A bits... per process.

#Matrix size:

The Matrix has as many trans tables as simultaneous processes are allowed (S). This is another trade-off situation. In this step we fix S seeking a comfortable value with acceptable cost in Matrix RAM.

M = N * S

The final size of the Matrix is M rows by A bits.

Let Main Memory be 2MB as the most. Therefore L = 21.

With such a small memory lets keep granularity high, say 1 KB per frame, that is: F = 1024.

#Linear Address fields:

d = log2 (F) = 10
P = L - d  = 21 - 10 = 11

#Matrix entry:

A = P  = 11

We have 4 control bits so the entry would be: 11 + 4 = 15 bits. Since this is kind of odd, we round to 16 bits and tell programmers we have let a "reserved bit", which sounds very technical.

#Trans Table size:

N = 2^P = 2048

So we have 2K x 16 bits (4KB) per process.

#Matrix size:

Let say we want to allow up to 128 simultaneous processes.

M = N * S = 2048 * 128 = 262,144

That is 256 Kwords (512 KB).

If we can afford to build this Matrix, then our system can be described as following:

- Main memory    : 2 MB max
- Sim. Processes : 128 max
- Matrix size    : 256K x 16 bits (512 KB).

(not too bad...)