Choques bidimensionales

Dinámica

Sistemas de partículas

Dinámica de un
sistema de partículas

Sistemas aislados

Choques frontales

Péndulo balístico

Choque entre una 
partícula y un bloque
unido a un muelle

Choques bidimensionales

Actividades

Carambola

El objetivo del programa interactivo es el de observar los choques bidimensionales de dos partículas en el sistema-L y en el sistema–C. Estudiaremos una situación más completa del choque entre dos discos en el capítulo Sólido rígido.

Fundamentos físicos

Supongamos que chocan dos discos o esferas de masas m₁ y m₂ y radios r₁ y r₂.

Se denomina parámetro de impacto b a la distancia entre la dirección de la velocidad del primer disco u1 y el centro del segundo disco que suponemos inicialmente en reposo.

La conservación del momento lineal respecto de los ejes X e Y orientados según se especifica en la figura se escribe

El coeficiente de restitución nos mide el cociente cambiado de signo, entre la velocidad relativa se separación a lo largo del eje X y la velocidad relativa de aproximación a lo largo del mismo eje.

Dado el parámetro de impacto b obtenemos el ángulo q . De la segunda y tercera ecuación podemos despejar el ángulo entre las direcciones de las velocidades de las partículas después del choque

La velocidad del centro de masas en el sistema de referencia X-Y de la figura es

Las velocidades de las partículas respecto del centro de masa son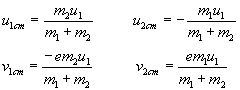

Como podemos fácilmente comprobar se cumple el principio de conservación del momento lineal en el sistema-C

La energía perdida en la colisión Q es la diferencia de las energías cinéticas después del choque y antes del choque bien referidas al sistema-L o al sistema-C. Pero es mucho más fácil calcular esta diferencia en el sistema-C.

Actividades

Para observar los choques bidimensionales, se introducen los siguientes parámetros en los correspondientes controles de edición

• El coeficiente de restitución, un valor comprendido entre 0 y 1. El valor de 1 corresponde a un choque elástico.
• El parámetro de impacto, un número comprendido entre 0 y 2, (se supone que las partículas son dos discos de radio unidad). El valor cero corresponde a los choques frontales.

• El cociente entre las masas m₂/m₁. Donde m₂ es la masa de la partícula que está inicialmente en reposo, y m₁ la masa de la partícula inicialmente en movimiento.

• La velocidad de la primera partícula u₁

Pulsamos el botón titulado Empieza, y observamos el choque en el sistema-L del laboratorio. Una cruz de color azul representa la posición del centro de masas del sistema formado por las dos partículas interactuantes. A la izquierda del applet observamos las energías de las partículas en un diagrama de tarta. Cuando el choque es elástico, la energía inicial es igual a la energía final. Cuando el choque es inelástico (coeficiente de restitución menor que la unidad) la energía inicial es mayor que la final.

Para observar el choque en el sistema-C activamos el botón de radio titulado S.R. C.M. Para volver al sistema-L activamos el botón de radio titulado S.R. Lab.

Se proporcionan los datos correspondientes a la velocidad de las partículas antes del choque y después del choque en el sistema–L, así como las direcciones de las partículas después del choque. Se representan también los momentos lineales en forma de vectores antes del choque y después del choque. De este modo el lector puede comprobar de forma visual la conservación del momento lineal.

La misma información que se proporciona del choque en el sistema-L también se proporciona en el sistema-C.

El botón titulado Pausa sirve para parar momentáneamente el movimiento, que se reanuda cuando se vuelve a pulsar el mismo botón titulado ahora Continua. Pulsando en el botón titulado Paso se observa la posición de las partículas en cada intervalo de tiempo, paso a paso.

Se recomienda al lector, que resuelva el mismo problemas de choques bidimensionales y compruebe su solución con el programa interactivo

Como ejemplo se recomienda aquél en el que las masas son iguales, la relación entre masas m₂/m₁ es igual a la unidad y el choque es elástico (e=1).

Carambola

Este programa es un juego que consiste en hacer una carambola. La bola roja se hace chocar con la azul y luego, ha de chocar con la bola de color gris.

Se pulsa el botón titulado Nuevo, y aparece las tres bolas en el recinto del applet.

Se pulsa el botón izquierdo del ratón cuando el puntero está sobre la bola roja y a continuación se arrastra, aparece una flecha que nos muestra el módulo y la dirección de la velocidad de la bola. Cuando se deja de pulsar el botón izquierdo del ratón la bola roja se mueve en dicha dirección. La longitud de la flecha determina el módulo de la velocidad de la bola roja.

Si no se ha acertado, se pulsa el botón titulado Inicio, para volver a situar las bolas en la posición de partida.

Como las bolas se distribuyen al azar en cada tercio horizontal del área de trabajo del applet, no todas las disposiciones tienen solución. Solamente se cuentan los choques de la primera bola con la segunda y a continuación, el choque de la primera con la tercera.