Dinámica general de la partícula

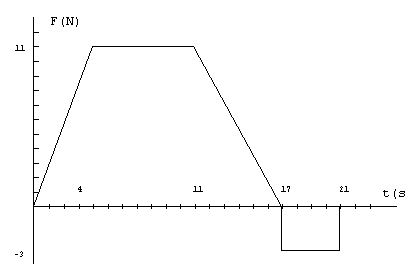1.-Gráfica de la fuerza aplicada a un móvil de 2 kg de masa en función del tiempo. Si la velocidad inicial del móvil (t=0) es de 2 m/s. Calcular: La velocidad del móvil en los instantes t = 4, 11, 17, 21, 24 s

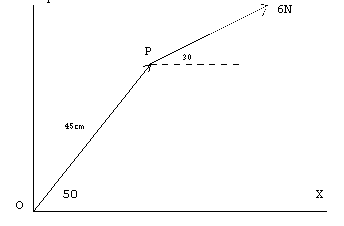2.-Hallar el momento (módulo dirección y sentido) de la fuerza F, de módulo 6N, respecto del origen

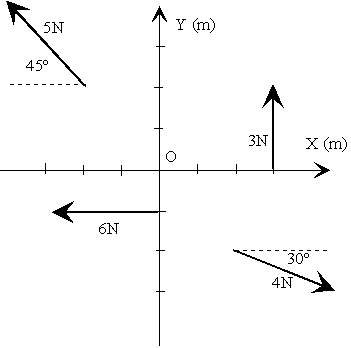3.-En el sistema de fuerzas de la figura Hallar la resultante El momento de cada fuerza respecto del origen El momento total

4.-Se dispara una bala de 200 g mediante un dispositivo desde la posición x= 20 cm, y=0, con velocidad de 100 m/s, haciendo un ángulo de 30 con el eje X. Hallar el momento angular respecto del origen, en el instante del lanzamiento.

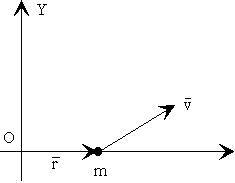
5.-Hallar el momento angular (módulo, dirección y sentido) de una partícula de masa m=2 kg que describe un movimiento circular en el plano XY en el sentido d elas agujas del reloj, de 40 cm de radio, con una velocidad angular de 50 r.p.m.

6.-Calcular el trabajo de una fuerza constante de 12 N, cuyo punto de aplicación se traslada 7 m, si el ángulo entre las direcciones de la fuerza y del desplazamiento son 0º, 60º, 90º, 135º, 180º

7.-Para alargar un muelle es necesario aplicar una fuerza

proporcional al desplazamiento F=Kx.

• Calcular el trabajo necesario para estirar un muelle 5 cm, si la constante del muelle es 1000 N/m.

8.-Un cuerpo de 4 kg de masa se mueve hacia arriba en un plano inclinado de 20º con respecto a la horizontal. Sobre el cuerpo actúan las siguientes fuerzas: una fuerza horizontal de 80 N, una fuerza paralela al plano de 100 N favoreciendo el movimiento, una fuerza de fricción de 10 N que se opone al movimiento. El cuerpo se traslada 20 m a lo largo del plano inclinado. Calcular:

• El valor de las fuerzas que faltan
• El trabajo de cada fuerza y el trabajo total.
• La resultante y el trabajo de la resultante.

9.-Un automóvil sube por una carretera de 3º de inclinación con una velocidad constante de 45 km/h. la masa del automóvil es de 1600 kg. Despreciar las fuerzas de fricción.

• ¿Cuál es la potencia desarrollada por el motor?
• ¿Cuál es el trabajo que ha efectuado en 10 s?

10.-Hallar la velocidad con que sale una bala después de haber atravesado una tabla de 7 cm de grosor y que opone una resistencia constante de 180 kgf. La velocidad inicial de la bala es de 450 m/s y su masa de 15 g. (Emplear dos métodos para resolver el problema: Dinámica y Teorema de la energía).

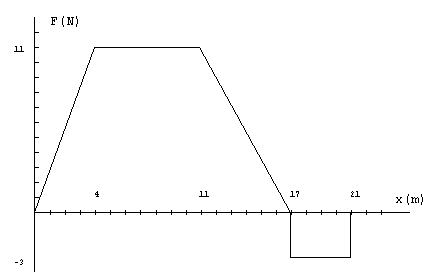11.-En la figura se muestra la gráfica de la fuerza aplicada a un móvil de 2 kg de masa en función del desplazamiento. Si la velocidad inicial del móvil (en x=0) es de 5 m/s. Calcular su velocidad en las posiciones x = 4, 11, 17, 21, 23.

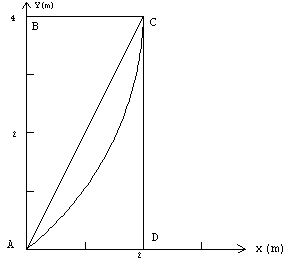12.-Sobre una partícula actúa una fuerza 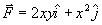Hallar el trabajo efectuado por la fuerza entre los puntos A y C a lo largo de los siguientes caminos: A - B - C. A - D - C. A largo de la recta que une A y C. A lo largo de la parábola y = x2 que pasa por dichos puntos.

13.-Un cuerpo de 2 kg se deja caer desde una altura de 3 m. Calcular:

• La velocidad del cuerpo en A, B y C., usando las fórmulas del movimiento rectilíneo uniformemente acelerado (caída de graves).
• La energía cinética, potencial y total en dichos puntos. ¿Se conserva la energía total?

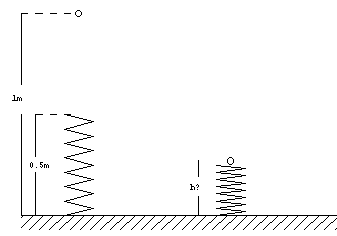14.-Se deja caer sobre un muelle en posición vertical una masa de 0.5 kg desde 1 m de altura. El muelle tiene una longitud de 0.5 m y una constante de 100 N/m. Calcular la longitud h del muelle cuando está comprimido al máximo

15.-Una bola de 5 kg de masa se lanza verticalmente hacia arriba con una velocidad inicial de 20 m/s, alcanza una altura de 15 m.

• Calcular la pérdida de energía debida a la resistencia del aire.

16.-Un bloque de masa 0.2 kg inicia su movimiento hacia arriba, sobre un plano de 30º de inclinación, con una velocidad inicial de 12 m/s. Si el coeficiente de rozamiento entre el bloque y el plano es de 0.16. Determinar:

• La longitud que recorre el bloque a lo largo del plano hasta que se para.
• La velocidad que tendrá el bloque al regresar a la base del plano.

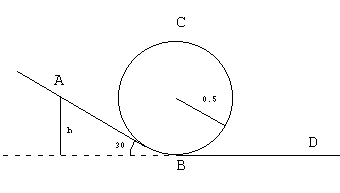17.-Un cuerpo de masa 2 kg y pequeñas dimensiones desliza por el raíl de la figura partiendo de A en reposo. Suponiendo que solo existe rozamiento en los planos inclinado y horizontal, y que el coeficiente de rozamiento vale 0.2, y el radio del bucle 0.5 m. Sabiendo que el cuerpo se encuentra inicialmente a h=2 m de altura sobre la horizontal, calcular: Las velocidades del cuerpo cuando pasa por B y C. La distancia BD recorrida por el cuerpo hasta pararse La reacción del raíl en las posiciones A, B, C, D.

18.-Un meteorito de 20000 T de masa se dirige desde el espacio exterior hacia la Tierra. Su velocidad a una distancia de 3.8 10⁷ m del centro de la Tierra es de 30 km/s. Calcular:

• La velocidad con que llegará a la superficie de la Tierra. (Se supone que la Tierra permanece inmóvil antes del choque).

Datos: masa de la Tierra 5.98 10²⁴ kg, radio 6370 km ,G=6.67 10^-11 N m²/kg²

19.-Determinar el módulo de la velocidad de un satélite artificial en órbita circular a una altura h, por encima de la superficie de la Tierra.

• Determinar el valor de h para un satélite geoestacionario (aquél cuya posición relativa respecto a la superficie de la Tierra permanece fija, es decir, su periodo es el mismo que el de la rotación de la tierra).

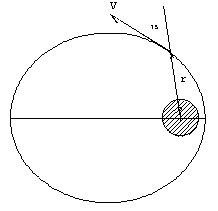20.-Un satélite artificial se lanza desde una altura de 2400 km de la superficie de la Tierra con una velocidad de 8000 m/s, formando un ángulo de 75º con la dirección radial, tal como se indica en la figura. Hallar: El momento angular y la energía total. La máxima y mínima altura del satélite

21.-Una partícula está sometida a una fuerza asociada a la energía potencial E_p=kx²/2.

• Representar la función
• Describir el movimiento de la partícula cuando su energía total E>0 (en qué región se puede mover, en qué posiciones la energía cinética (velocidad) es máxima y en qué posiciones es mínima, etc.)
• Dibujar la fuerza sobre la partícula en x=0, en una posición x<0 y en otra posición x>0.
• ¿Cuál es la posición de equilibrio estable?

22.-Una partícula está sometida a una fuerza asociada a la energía potencial E_p(x)=3x²-x³.

• Representar la función.
• Determinar los intervalos a lo largo del eje X en los que la partícula puede moverse, si su energía total vale: (a) E=–16, (b) E=2, (c) E=20.
• Hallar la expresión de la fuerza que actúa sobre la partícula. Calcularla y representarla en las posiciones x=-2, x=1, x=4.
• Determinar las posiciones de equilibrio estable e inestable.
• Calcular el valor de la energía cinética y potencial de un móvil cuya energía total es E=20, en las posiciones x=0, x=-2, y x=2.