Interacción electrostática en el vacío

1.-Calcular el cociente entre la fuerza eléctrica y gravitacional entre dos electrones.

Datos: G = 6.67 10^-11 Nm²/kg², carga electrón = 1.6 10^-19 C, masa electrón = 9.1 10^-31 kg

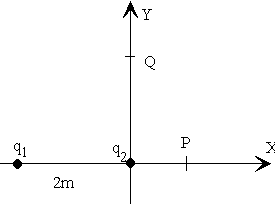
2.-Calcular el campo eléctrico y el potencial del sistema de cargas de la figura en P y en Q. Datos: q1=28 10-9 C, q2=-16 10-9 C, Puntos P(1, 0), y Q(0,1.5) metros

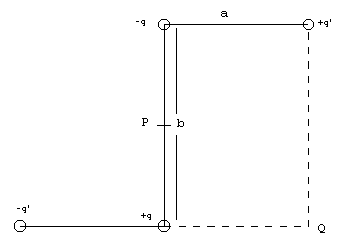3.-Dado el sistema de cargas de la figura, calcular el valor de q para que el campo en P sea horizontal. Luego hallar: El campo en Q El potencial en P y en Q. Determinar el trabajo que es necesario realizar para mover una carga de 4 mC entre P y Q. Datos: a =12cm, b=20cm, q'=3mC

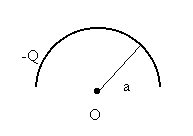4.-Calcular el campo eléctrico (módulo, dirección y sentido) creado por un hilo en forma semicircular de radio a, cargado con una carga -Q, en su centro. Calcular, también, el potencial en el centro del semicírculo.

5.-Calcula el campo creado por un hilo indefinido y rectilíneo cargado con una densidad de carga de l C/m. a una distancia R del hilo.

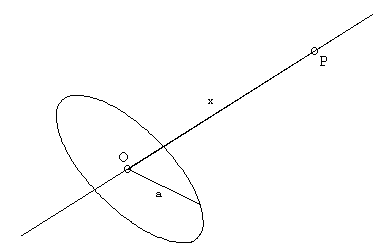6.-Calcula el campo eléctrico y el potencial creado por un anillo, de radio a, cargado con carga q, en un punto P del eje del anillo situado a una distancia x de su centro.

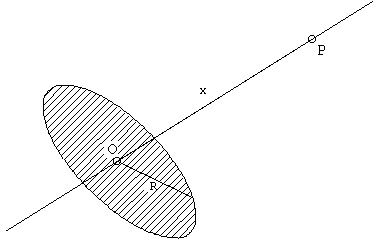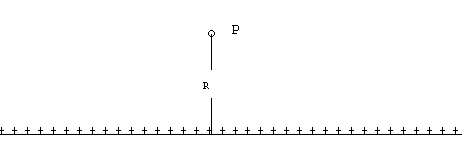
7.-Hallar el campo eléctrico creado en el punto P del eje de un disco circular de radio R uniformemente cargado con una densidad de carga de s C/m2. Determinar el módulo y dirección del campo eléctrico cuando R tiende a infinito, es decir, cuando el disco se convierte en una placa plana e indefinida cargada.

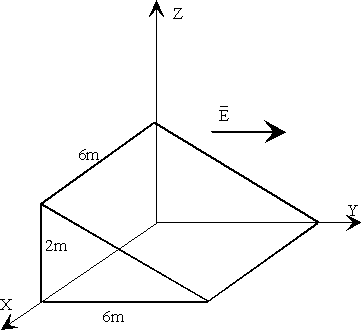8.-Calcular el flujo del campo eléctrico paralelo al eje Y A través de cada una de las caras del poliedro El flujo total a través de la superficie del poliedro.

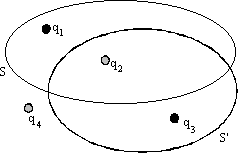9.-Calcular el flujo del campo eléctrico a través de la superficies cerradas S y S', para los siguientes valores de las cargas. q1=2 10-9 C, q2=-3 10-9 C, q3=5 10-9 C, q4=-4 10-9 C.

10.-Hállese el flujo del campo eléctrico a través de una superficie esférica de radio r que tiene una carga puntual q situada en su centro

11.-Hállese el flujo del campo eléctrico producido por un hilo rectilíneo e indefinido cargado con una densidad de carga de l C/m, a través de una superficie cilíndrica de radio R y de longitud L, estando situado el hilo cargado en el eje del cilindro. (Véase el problema 5)

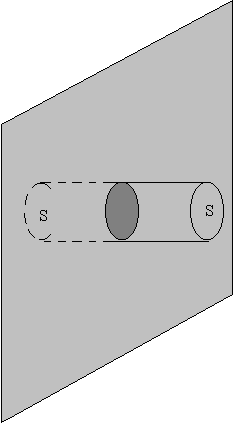12. Hállese el flujo del campo eléctrico producido por una distribución plana e indefinida de carga de s C/m2, a través de la superficie cilíndrica mostrada en la figura.

13.-Una esfera de 5 cm de radio está uniformemente cargada con una carga Q= 2 10^-6 C.

• ¿Cuál es la dirección y sentido del campo eléctrico?
• Calcular el módulo del campo eléctrico en el interior (r<5), y en el exterior (r>5)de la esfera cargada, a una distancia r del centro de la esfera.

14.- Un cilindro muy largo, macizo, de 5 cm de radio está uniformemente cargado en todo su volumen con una densidad de carga de 4 10^-6 C/m³.

• Determinar, razonadamente, la expresión del campo eléctrico dentro y fuera del cilindro.

Determinar la diferencia de potencial entre un punto situado en el eje del cilindro y otro a 15 cm del mismo.

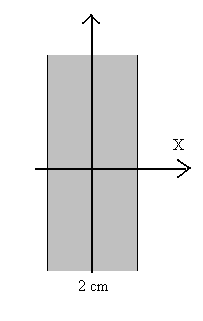15.-Una placa plana, indefinida de 2 cm de espesor, está uniformemente cargada, con una densidad de carga de 2 10-8 C/m3. Obtener razonadamente la expresión del campo eléctrico en el interior y en el exterior de dicha placa. Representar el módulo del campo eléctrico en función de la distancia a la placa. Hallar la diferencia de potencial entre el origen (plano que divide a la placa por la mitad) y un punto situado a 8 cm de dicho plano.