Movimiento del sólido rígido



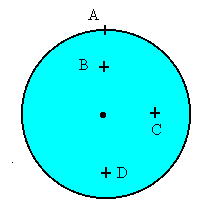 |
 1.-Hallar
y dibujar el vector velocidad de los puntos del disco que se indican en la figura. El
disco rueda sin deslizar, tiene un radio de 5 cm, y se mueve (su c.m.) con velocidad de
3m/s. A está en la periferia, y B (arriba), C (a la derecha), y D (abajo) están a 2.5 cm
del centro. 1.-Hallar
y dibujar el vector velocidad de los puntos del disco que se indican en la figura. El
disco rueda sin deslizar, tiene un radio de 5 cm, y se mueve (su c.m.) con velocidad de
3m/s. A está en la periferia, y B (arriba), C (a la derecha), y D (abajo) están a 2.5 cm
del centro. |
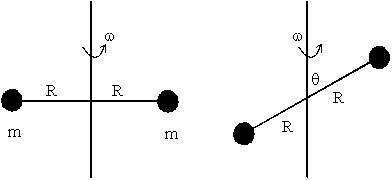 |
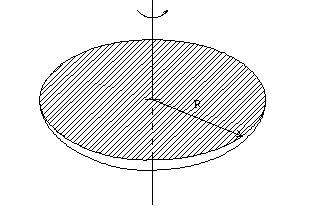
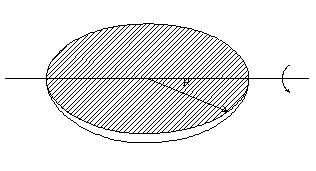
 2.-Determinar,
el módulo, dirección y sentido del vector momento angular, en cada uno de los casos
mostrados en la figura. 2.-Determinar,
el módulo, dirección y sentido del vector momento angular, en cada uno de los casos
mostrados en la figura. Calcúlese el momento de inercia respecto del eje de rotación |
 3.-Una varilla
delgada de 1 m de largo tiene una masa despreciable. Se colocan 5 masas de 1 kg cada una,
situadas a 0, 25cm, 50 cm, 75 cm, y 100 cm de uno de sus extremos. Calcular el momento de
inercia del sistema con respecto a un eje perpendicular a la varilla el cual pasa a
través:
3.-Una varilla
delgada de 1 m de largo tiene una masa despreciable. Se colocan 5 masas de 1 kg cada una,
situadas a 0, 25cm, 50 cm, 75 cm, y 100 cm de uno de sus extremos. Calcular el momento de
inercia del sistema con respecto a un eje perpendicular a la varilla el cual pasa a
través:
- De un extremo
- De la segunda masa
- Del centro de masa
- Comprobar el teorema de Steiner
 4.-Calcular el
momento de inercia de los siguientes cuerpos de masa M y de dimensiones que se indican,
respecto del eje señalado en la figura.
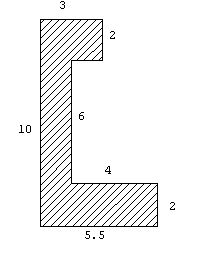
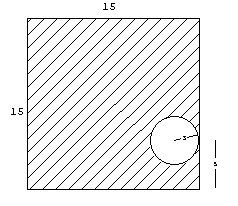
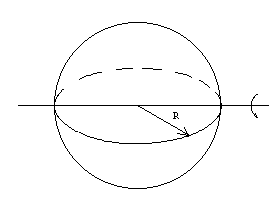
4.-Calcular el
momento de inercia de los siguientes cuerpos de masa M y de dimensiones que se indican,
respecto del eje señalado en la figura.
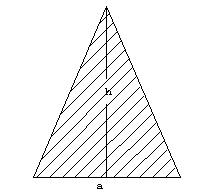
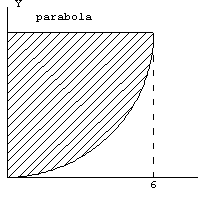
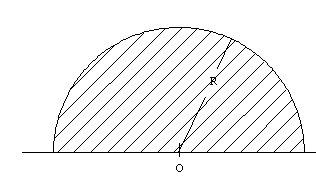
 5.-Determinar
la posición del centro de masa de las siguientes figuras planas y homogéneas 5.-Determinar
la posición del centro de masa de las siguientes figuras planas y homogéneas |
 |
 |
 |
 |
 |
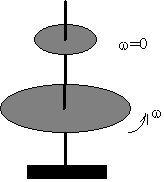 |
 6.-Un
disco homogéneo puede girar alrededor de un eje vertical a 90 r.p.m. Su masa es de 25 kg
y el diámetro 1 m. Se acopla otro disco coaxial de 50 kg de masa y 50 cm de diámetro. 6.-Un
disco homogéneo puede girar alrededor de un eje vertical a 90 r.p.m. Su masa es de 25 kg
y el diámetro 1 m. Se acopla otro disco coaxial de 50 kg de masa y 50 cm de diámetro.
- Calcular la velocidad angular del conjunto
La energía perdida en el acoplamiento. |
 |
 7.-Una
bala de 0.2 kg y velocidad horizontal de 120 m/s, choca contra un pequeño diente situado
en la periferia de un volante de masa 1.5 kg y 12 cm de radio, empotrándose en el mismo.
Suponiendo que la bala es una masa puntual, que el volante es un disco macizo y homogéneo
(no se tiene en cuenta el pequeño diente). Calcular: 7.-Una
bala de 0.2 kg y velocidad horizontal de 120 m/s, choca contra un pequeño diente situado
en la periferia de un volante de masa 1.5 kg y 12 cm de radio, empotrándose en el mismo.
Suponiendo que la bala es una masa puntual, que el volante es un disco macizo y homogéneo
(no se tiene en cuenta el pequeño diente). Calcular:
- La velocidad angular adquirida por el sistema disco - bala después del choque
- La pérdida de energía resultante
|
 8.-Un disco que
gira está sometido a un momento de 10 Nm, debido a la fricción en su eje. El radio del
disco es de 0.6 m y su masa de 100 kg, y estaba girando inicialmente a 175 rad/s. Hallar:
8.-Un disco que
gira está sometido a un momento de 10 Nm, debido a la fricción en su eje. El radio del
disco es de 0.6 m y su masa de 100 kg, y estaba girando inicialmente a 175 rad/s. Hallar:
- ¿Cuánto tiempo tardará en detenerse?
- ¿Cuántas vueltas dará hasta que se para?
- Hallar el trabajo efectuado por la fuerza y la variación de energía cinética.
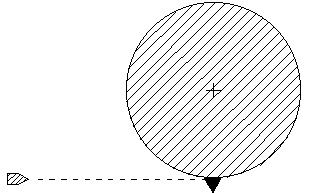
 |
 9.-La
rueda de la figura tiene un radio de 0.5 m y una masa de 25 kg. Puede girar en torno a un
eje horizontal. De la cuerda enrollada en la periferia pende una masa de 10 kg. Calcula: 9.-La
rueda de la figura tiene un radio de 0.5 m y una masa de 25 kg. Puede girar en torno a un
eje horizontal. De la cuerda enrollada en la periferia pende una masa de 10 kg. Calcula:
- La aceleración angular de la rueda
- La aceleración del cuerpo
- La tensión de la cuerda
- La velocidad de la masa una vez ha descendido dos metros partiendo del reposo (emplea
dos métodos de cálculo para este apartado).
|
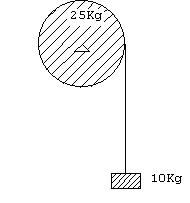
 |
 10.-El
sistema de la figura consta de una polea formada por dos discos coaxiales soldados de
masas 550 y 300 g y radios 8 y 6cm, respectivamente. Dos masas de 600 y 500 g cuelgan del
borde de cada disco. Calcular: 10.-El
sistema de la figura consta de una polea formada por dos discos coaxiales soldados de
masas 550 y 300 g y radios 8 y 6cm, respectivamente. Dos masas de 600 y 500 g cuelgan del
borde de cada disco. Calcular:
- La tensión de cada cuerda
- La aceleración de cada masa
La velocidad de cada cuerpo cuando uno de ellos (¿cuál?) haya descendido 3 m
partiendo del reposo (emplea dos procedimientos de cálculo). |
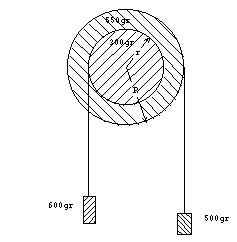
 |
 11.-Enrollamos
una cuerda a un cilindro macizo y homogéneo de 10 kg y el otro extremo de la cuerda la
fijamos al techo, tal como se indica en la figura. Soltamos el sistema partiendo del
reposo de forma que al caer la cuerda va desenrollándose. Calcular: 11.-Enrollamos
una cuerda a un cilindro macizo y homogéneo de 10 kg y el otro extremo de la cuerda la
fijamos al techo, tal como se indica en la figura. Soltamos el sistema partiendo del
reposo de forma que al caer la cuerda va desenrollándose. Calcular:
- La aceleración del c.m. del disco
- La tensión de la cuerda.
- La velocidad del c.m. del cilindro cuando haya descendido dos metros, (emplea dos
procedimientos de cálculo).
|
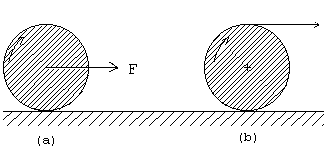 |
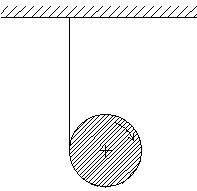
 12.-Un
cilindro macizo de masa M y radio R se le aplica una fuerza F tal como indica la figura.
Calcular en cada caso (a) y (b): 12.-Un
cilindro macizo de masa M y radio R se le aplica una fuerza F tal como indica la figura.
Calcular en cada caso (a) y (b):
La fuerza de rozamiento para que ruede sin deslizar |
 13.-Un cuerpo de 20
kg baja deslizando a lo largo de un plano inclinado 30º respecto a la horizontal, y de 10
m de longitud. Suponiendo que el coeficiente de rozamiento entre el cuerpo y el plano es
0.2. Calcular:
13.-Un cuerpo de 20
kg baja deslizando a lo largo de un plano inclinado 30º respecto a la horizontal, y de 10
m de longitud. Suponiendo que el coeficiente de rozamiento entre el cuerpo y el plano es
0.2. Calcular:
- El tiempo que tardará en recorrerlo y la velocidad con que llegará al final del plano
- Si el cuerpo tiene forma esférica y baja rodando (sin deslizar) ¿Con qué velocidad
llegará al final del plano inclinado? (radio de la esfera 10 cm.)
- Explicar en cada uno de los casos en qué se transforma la energía potencial inicial
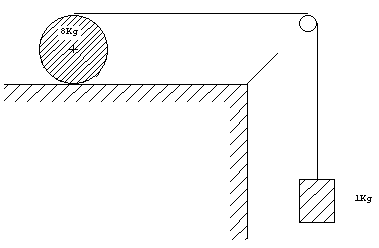 |
 14.-Calcular
la aceleración del bloque, del c.m. del disco, y la tensión de la cuerda, suponiendo que
el disco tiene un radio de 30 cm y rueda sin deslizar sobre el plano horizontal, la polea
tiene una masa despreciable. 14.-Calcular
la aceleración del bloque, del c.m. del disco, y la tensión de la cuerda, suponiendo que
el disco tiene un radio de 30 cm y rueda sin deslizar sobre el plano horizontal, la polea
tiene una masa despreciable.Calcúlese la velocidad del bloque una vez que haya
descendido 2 m partiendo del reposo. (Emplear dos procedimientos para el cálculo de este
apartado). |


![]() 3.-Una varilla
delgada de 1 m de largo tiene una masa despreciable. Se colocan 5 masas de 1 kg cada una,
situadas a 0, 25cm, 50 cm, 75 cm, y 100 cm de uno de sus extremos. Calcular el momento de
inercia del sistema con respecto a un eje perpendicular a la varilla el cual pasa a
través:
3.-Una varilla
delgada de 1 m de largo tiene una masa despreciable. Se colocan 5 masas de 1 kg cada una,
situadas a 0, 25cm, 50 cm, 75 cm, y 100 cm de uno de sus extremos. Calcular el momento de
inercia del sistema con respecto a un eje perpendicular a la varilla el cual pasa a
través:
![]() 4.-Calcular el
momento de inercia de los siguientes cuerpos de masa M y de dimensiones que se indican,
respecto del eje señalado en la figura.
4.-Calcular el
momento de inercia de los siguientes cuerpos de masa M y de dimensiones que se indican,
respecto del eje señalado en la figura.







![]() 8.-Un disco que
gira está sometido a un momento de 10 Nm, debido a la fricción en su eje. El radio del
disco es de 0.6 m y su masa de 100 kg, y estaba girando inicialmente a 175 rad/s. Hallar:
8.-Un disco que
gira está sometido a un momento de 10 Nm, debido a la fricción en su eje. El radio del
disco es de 0.6 m y su masa de 100 kg, y estaba girando inicialmente a 175 rad/s. Hallar:




![]() 13.-Un cuerpo de 20
kg baja deslizando a lo largo de un plano inclinado 30º respecto a la horizontal, y de 10
m de longitud. Suponiendo que el coeficiente de rozamiento entre el cuerpo y el plano es
0.2. Calcular:
13.-Un cuerpo de 20
kg baja deslizando a lo largo de un plano inclinado 30º respecto a la horizontal, y de 10
m de longitud. Suponiendo que el coeficiente de rozamiento entre el cuerpo y el plano es
0.2. Calcular:
