Estática

Estática

1.-Calcular el peso P necesario para mantener el equilibrio en el sistema mostrado en la figura. En el cual A pesa 100 kg, Q pesa 10 kg. El plano y las poleas son lisas. La cuerda AC es horizontal y la cuerda AB es paralela al plano.

Calcular también la reacción del plano sobre el cuerpo A.

2.-Dos cilindros macizos y homogéneos de pesos 6 y 10 kg se apoyan sin rozamiento sobre los planos inclinados de la figura. Calcular:

El ángulo que forma con la horizontal la línea que une los centros de los dos cilindros.
La reacción de los planos inclinados

3.-Una viga uniforme tiene 4 m de larga y pesa 100 Kg. Un hombre de 75 kg está situado a 1 m del apoyo A.

Calcula las reacciones en los apoyos A y B.

4.-Una varilla de 6 kg y 0.8 m de longitud está apoyada sobre un ángulo recto liso, como se muestra en la figura. Calcular :

El ángulo de equilibrio que forma la varilla con la horizontal.
Las reacciones en los apoyos.

5.-Una escalera, de masa 40 kg y 6 m de longitud, está apoyada sobre una pared lisa vertical y sobre un suelo horizontal rugoso (m=0.4). Calcular:

La fuerza de rozamiento cuando el un hombre de 80 kg ha subido 3 m a lo largo de la escalera.
La longitud máxima a lo largo de la escalera a la que puede ascender, antes de que comience a deslizar.

6.-Queremos arrastrar una silla a velocidad constante sobre el suelo horizontal, siendo el coeficiente dinámico de rozamiento entre las patas y el suelo 0.3. La silla pesa 25 kg.

¿Cuál es la fuerza horizontal F, aplicada a 0.6 m de altura sobre el suelo, necesaria para arrastrarla?. ¿Cuánto vale la reacción del suelo sobre las patas delanteras y traseras?.

¿A qué altura máxima se podrá aplicar la fuerza de arrastre sin que vuelque la silla?

7.-Una pluma de 4 m de la grúa de la figura pesa 200 kg y está sosteniendo una carga de 1000 kg. Calcular:

La tensión del cable AB y las componentes de la fuerza sobre la articulación C.

8.-Calcular el peso máximo del disco de la figura, sabiendo que la tensión máxima que puede soportar la cuerda es de 15 kg.

Calcular también la reacción en la articulación A
Datos: peso de la barra 6 kg, longitud 40 cm; radio del disco 20 cm.

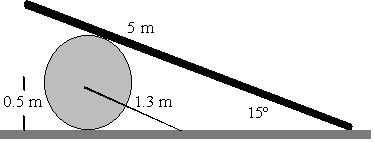
9.-En el problema esquematizado en la figura, la barra tiene una longitud de 5 m y pesa 20 kg, el cilindro tiene un peso de 30 kg y un radio de 0.5 m. Suponer que no hay rozamiento entre la barra y el cilindro, y que el coeficiente est tico de rozamiento entre el extremo derecho de la barra y el plano horizontal es 0.3. La esfera está sujeta, a su vez, por una cuerda de 1.3 m de longitud.

Calcular la fuerza de rozamiento y la tensión de la cuerda cuando el ángulo entre la barra y el plano horizontal es de 15º.
¿Deslizará o no la barra?, razonar la respuesta.

10.-Una barra OA de 30 kg de peso y 2 m de longitud, articulada en O, se apoya sobre una caja rectangular de 10 kg de peso y de dimensiones 0.75 y 0.5 m. La caja puede deslizar sobre el plano horizontal. Sabiendo que el ángulo entre la barra y el plano horizontal es de 30º, calcular:

La fuerza sobre la articulación O
La fuerza que ejerce plano horizontal sobre la caja y su punto de aplicación.
¿Deslizará o no la caja?. Razona la respuesta.

Dato: el coeficiente estático de rozamiento entre la caja y el plano horizontal vale 0.5

11.-Dos escaleras CA y DA de 40 kg y 30 kg, respectivamente, se apoyan sobre un suelo liso y se articulan en el vértice A, están sujetas por una cuerda paralela al suelo situada a 0.9 m del mismo. Las escaleras forman entre sí un ángulo recto. Calcular:

Las reacciones en los apoyos C y B.
La tensión de la cuerda.

Las componentes horizontal y vertical de la fuerza que una escalera ejerce sobre la otra a través de la articulación A.