 FOTOELEC FOTOELEC
El simula el efecto fotoeléctrico. Se dispone de un conjunto de
lámparas monocromáticas y de metales para ser iluminados. Se selecciona un metal y una
lámpara, si la energía de los fotones es superior a la energía de arranque podemos
observar un electrón saliendo de la placa iluminada. Se tratará de establecer una
diferencia de potencial entre las placas de modo que el electrón emitido llegue justo a
la placa opuesta. En caso de que el fotón no tenga suficiente energía, se selecciona
otra lámpara y así sucesivamente.
En esta situación se toman los datos de la longitud de onda de la
radicación y de la diferencia de potencial, y se guardan en la caja de listas situada a
la izquierda de la ventana. En esta experiencia simulada, se examina también el papel de
la intensidad de la luz que ilumina la placa metálica.
Una vez recolectados los datos, el programa realiza el tratamiento de
los mismos. A partir del gráfico potencial de detención-frecuencia de la luz que ilumina
la placa, se determina la energía de arranque de los electrones del metal, y la constante
h de Planck.
 DIFRACCI DIFRACCI
Se estudia la difracción de micropartículas o fotones que inciden uno
a uno sobre una rendija estrecha, cuya anchura se puede modificar.
Se sitúan detectores en una pantalla paralela a la rendija. Cada vez
que un detector registra una micropartícula, incrementa en una unidad su contador
interno. Una gráfica en forma de barras visualiza en cada instante el número de cuentas
de cada detector.
Cuando el número de micropartículas incidentes es grande el diagrama
de barras se aproxima a la representación de la función de la intensidad de la
difracción Fraunhofer por una rendija estrecha. Se concluye que la difracción es un
fenómeno colectivo, que el comportamiento de una partícula individual en el dominio
cuántico es imprevisible, y que por tanto, no tiene sentido el hablar de la trayectoria
de una micropartícula. A partir de esta representación gráfica, se puede explicar
fácilmente la relación de incertidumbre posición - momento.
 ESCALON1 ESCALON1
Una micropartícula de energía mayor que la del escalón incide sobre la frontera que
separa las dos regiones de distinto potencial. No se puede predecir de antemano si la
partícula se reflejará o se transmitirá.
Sin embargo, podemos predecir la conducta de un número grande de
micropartículas, calculando el coeficiente de reflexión o transmisión a partir de la
solución de la ecuación de Schrödinger para un escalón de potencial
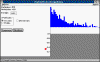 ESCALON2 ESCALON2
Se trata del segundo caso de la aplicación de la ecuación de
Schrödinger al escalón de potencial. Las predicciones de la Mecánica Cuántica difieren
substancialmente de la Mecánica Clásica.
Hay una cierta probabilidad de encontrar la micropartícula a una
cierta distancia en el interior de la región clásicamente prohibida. Esta probabilidad
es tanto menor cuanto mayor es la masa de la micropartícula. Este ejemplo, nos permite
introducir al efecto túnel, es decir, la transmisión de micropartículas al otro lado de
la barrera de potencial a través de la región clásicamente prohibida.
 NUCLEO NUCLEO
El efecto túnel explica la desintegración radioactiva, es decir, la
emisión de partículas alfa por núcleos inestables.
Un modelo simplificado de núcleo consistente en dos barreras de
potencial entre las cuales se mueve hacia adelante y hacia atrás una partícula alfa. La
probabilidad de que la partícula alfa atraviese la barrera de potencial por efecto túnel
disminuye fuertemente con la anchura de la barrera.
 RADIACT1 RADIACT1
Se estudia la desintegración de una sustancia radioactiva en otra
estable.
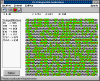
En la ventana se sitúan una muestra de núcleos radioactivos A,
que al desintegrarse se convierten en núcleos estables B. Una vez que se pone en
marcha el programa, cada cierto tiempo se toman datos del número de núcleos que
permanecen sin desintegrar y del tiempo, y se guardan en la caja de listas situada a la
izquierda de la ventana. Una vez recolectados suficientes datos, se representan en una
gráfica comprobándose que siguen una ley exponencial decreciente.
Se podrá comprobar que no se puede predecir qué núcleo se
desintegrará y en qué momento, sin embargo, la conducta del conjunto de núcleos a lo
largo del tiempo, sigue aproximadamente una exponencial decreciente.
Una facetas más interesantes del programa es que el estudiante tiene
que aprender a tomar datos en una determinada secuencia para definir bien la ley
exponencial.
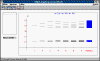
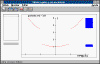
 POZO POZO
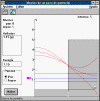
El objetivo de este programa es el de explicar el concepto de nivel de
energía y función de onda.
El estudiante ha de buscar los niveles de energía de un pozo de
potencial, con el criterio de que la solución de la ecuación de Schrödinger para una
determinada energía es una función de onda cuando tiende asintóticamente a cero al
hacerse x grande. También, ha prestar atención a la simetría de las funciones de
onda, y al número de veces que corta al eje horizontal.
  SOLIDO SOLIDO
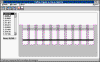
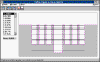
Se estudia los niveles de energía y las funciones de onda de un
conjunto de hasta 10 pozos de potencial, y el potencial periódico denominado modelo de
Koning-Penney.
Un pozo representa un modelo de átomo. Dos pozos representan un modelo
de molécula diatómica. En base a este modelo se explica el enlace covalente.
Un conjunto de pozos representa un modelo de sólido lineal. Podemos
apreciar el proceso de formación de bandas de energía a medida que se incrementa el
número de átomos de la cadena lineal. La forma de las funciones de onda, y las
denominadas zonas de Brillouin en la representación energía-número de onda.
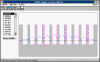
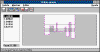
Se observa la modificación de los niveles de energía y de las
funciones de onda de una cadena de átomos por la introducción de un defecto central.
Este defecto puede ser bien un pozo cuya anchura y/o profundidad se han modificado, o una
barrera cuya anchura y/o altura se ha incrementado o disminuido.
 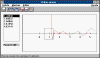 AMORFO AMORFO
Estudia los niveles de energía y funciones de onda asociados de un
sistema irregular de pozos de potencial.
El programa calcula los niveles de energía, aunque también es posible
buscarlos de forma manual.
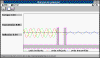 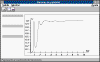 TRANSMIS TRANSMIS
Representa la función de onda incidente, reflejada o trasnmitida por
una o más barreras de potencial.
Representa el coeficiente de transmisión en función de la energía de
las partículas. El programa tiene la opción de ampliar zonas de dicha representación
gráfica a fin de examinar las energías correspondientes a los picos de resonancia. |