 OSCILACI1 OSCILACI1
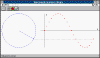
El propósito del programa es el de establecer la relación entre el
Movimiento Armónico Simple y el movimiento circular uniforme.
Se introduce la amplitud, frecuencia angular, y fase inicial. Se
observa la proyección del extremo del vector rotatorio sobre el eje X, trazándose la
posición del móvil en función del tiempo (parte derecha de la ventana).
 OSCILACI2 OSCILACI2
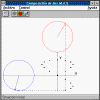
Explica el procedimiento para componer dos M.A.S. de direcciones
perpendiculares en base a la relación entre el Movimiento Armónico Simple y el
movimiento circular uniforme.
Se introduce la frecuencia angular de cada unos de los M.A.S. y el
desfase entre ambos, y se observa la trayectoria del móvil en el plano X-Y.
 OSCILA3 OSCILA3
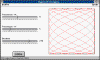
Obtiene las figuras de Lissajous, representando la trayectoria seguida
por una partícula sometida a dos M.A.S. de direcciones perpendiculares, de distinta
frecuencia y fase inicial.
Con los controles deslizantes de la parte izquierda se establece la
frecuancia de cada unos de los dos M.A.S., y el desfase entre ambos. Pulsando en el botón
Gráfica, se dibuja la trayectoria. Las figuras de Lissajous están contenidas en
un rectángulo de dimensiones iguales al doble de la amplitud. Los lados del rectángulo
son tangentes a la curva en un número de puntos y la razón del número de estos puntos
tangenciales a lo largo del eje X a aquellos a lo largo del eje Y es inversa de la razón
de las correspondientes frecuencias.
 FORZADAS FORZADAS
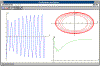
Se estudia el oscilador libre, amortiguado y forzado en tres dominios
distintos de representación: la posición del móvil en función del tiempo, la energía
en función del tiempo, y la trayectoria del móvil en el espacio de las fases.
En el caso del oscilador libre podemos apreciar que la amplitud no
cambia, la energía del oscilador es constante, y describe una trayectoria elíptica en el
espacio de las fases.
En el caso del oscilador amortiguado, la amplitud decrece
exponencialmente con el tiempo, la energía disminuye, y describe una trayectoria en forma
de espiral en el espacio de las fases. Asimismo, se pueden estudiar los casos de
oscilaciones críticas y sobreamortiguadas.
En el caso del oscilador forzado, se estudia el estado transitorio y su
dependencia de las condiciones iniciales y del rozamiento. Se estudia el estado
estacionario (si es que se alcanza), en la resonancia o cerca de la misma. Se comprueba la
necesidad de calcular valores medios durante el periodo de una oscilación en la
representación de la energía en función del tiempo. |