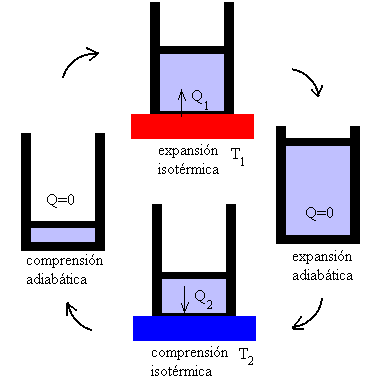
| Se define ciclo de Carnot como un proceso cíclico reversible que
utiliza un gas perfecto, y que consta de dos transformaciones isotérmicas y dos
adiabáticas, tal como se muestra en la figura.
La representación gráfica del ciclo de Carnot en un diagrama p-V es el siguiente
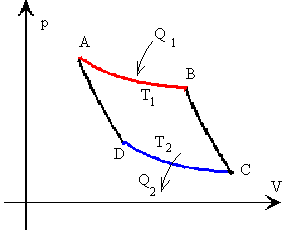 |
Tramo A-B isoterma a la temperatura T1 Tramo B-C
adiabática
Tramo C-D isoterma a la temperatura T2
Tramo D-A adiabática |
En cualquier ciclo, tenemos que obtener a partir de los datos iniciales:
- La presión, volumen de cada uno de los vértices.
- El trabajo, el calor y la variación de energía interna en cada una de las etapas.
- El trabajo total, el calor absorbido, el calor cedido, y el rendimiento del ciclo.
Los datos iniciales son los que figuran en la tabla adjunta. A partir de estos datos,
hemos de rellenar los huecos de la tabla.
| Variables |
A |
B |
C |
D |
| Presión p (atm) |
pA |
|
|
|
| Volumen v (l) |
vA |
vB |
|
|
| Temperatura T (ºK) |
T1 |
T1 |
T2 |
T2 |
Para obtener las variables y magnitudes desconocidas haremos uso de las fórmulas que
figuran en el cuadro-resumen
de las transformaciones termodinámicas.
- Transformación A->B (isoterma)
La presión pB se calcula a partir de la ecuación del gas ideal 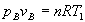
Variación de energía interna 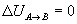
Trabajo 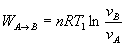
Calor 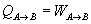
- Transformación B->C (adibática)
La ecuación de estado adiabática es 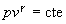 o bien, o bien, 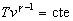 . Se despeja vc de la ecuación de la
adiabática . Se despeja vc de la ecuación de la
adiabática 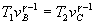 . Conocido vc
y T2 se obtiene pc, a partir de la ecuación del gas
ideal. . Conocido vc
y T2 se obtiene pc, a partir de la ecuación del gas
ideal. 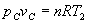 . .
Calor 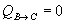
Variación de energía interna 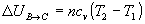
Trabajo 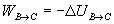
- Transformación C->D (isoterma)
Variación de energía interna 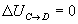
Trabajo 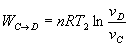
Calor 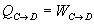
- Transformación D-> A (adibática)
Se despeja vD de la ecuación de la adiabática 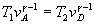 . Conocido vD y T2
se obtiene pD, a partir de la ecuación del gas ideal. . Conocido vD y T2
se obtiene pD, a partir de la ecuación del gas ideal. 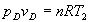 . .
Calor 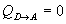
Variación de energía interna 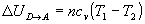
Trabajo 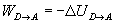
- Variación de energía interna
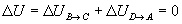
En un proceso cíclico reversible la variación de energía interna es cero
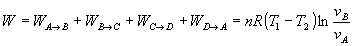
Los trabajos en las transformaciones adiabáticas son iguales y opuestos. Por otra
parte, podemos establecer a partir de las ecuaciones de las dos adiabáticas la relación
entre los volúmenes de los vértices
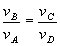 lo que nos conduce a la expresión final del
trabajo total del ciclo lo que nos conduce a la expresión final del
trabajo total del ciclo
En la isoterma T1 se absorbe calor Q>0 ya que vB>vA
de modo que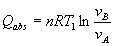
En la isoterma T2 se cede calor Q<0 ya que vD<vC
Se define rendimiento como el cociente entre el trabajo realizado y el calor absorbido
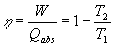
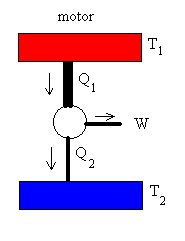 |
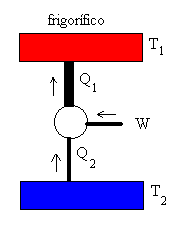
Un motor de Carnot es un dispositivo ideal que describe un ciclo de
Carnot. Trabaja entre dos focos, tomando calor Q1 del foco caliente a
la temperatura T1, produciendo un trabajo W, y cediendo un
calor Q2 al foco frío a la temperatura T2. En un
motor real, el foco caliente está representado por la caldera de vapor que suministra el
calor, el sistema cilindro-émbolo produce el trabajo, y se cede calor al foco frío
que es la atmósfera. |
 |
La máquina de Carnot también puede funcionar en sentido inverso,
denominándose entonces frigorífico. Se extraería calor Q2 del foco
frío aplicando un trabajo W, y cedería Q1 al foco caliente.
En un frigorífico real, el motor conectado a la red eléctrica produce un trabajo que
se emplea en extraer un calor del foco frío (la cavidad del frigorífico) y se cede calor
al foco caliente, que es la atmósfera. |
Introducir los valores de las siguientes variables
- Temperatura del foco caliente T1
- Temperatura del foco frío T2
Se tiene que cumplir que T1> T2
- El volumen de A, vA,
- El volumen de B, vB.
Se tiene que cumplir que vA< vB
Si no se cumplen las condiciones anteriores un mensaje nos lo señala en el borde
inferior del applet.
Una vez introducidos los datos se pulsa el botón titulado Empieza, el programa
interactivo calcula:
- La presión y el volumen de cada uno de los restantes vértices
- El trabajo, calor y variación de energía interna en cada una de las transformaciones
- El trabajo total , el calor absorbido y el calor cedido.
|