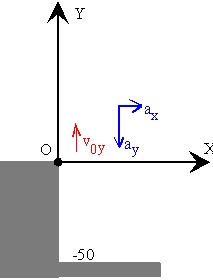
Se lanza una pelota verticalmente hacia arriba con una velocidad de 20 m/s desde la azotea de un edificio de 50 m de altura. La pelota además es empujada por el viento, produciendo un movimiento horizontal con una aceleración de 2 m/s2. Calcular:
Ecuaciones del movimiento rectilíneo uniformemente acelerado
Movimiento de caída de los cuerpos
Alcance horizontal x=3.03 m
La altura desde el suelo es 70 m
Cuando el móvil se encuentra a 60 m de altura
Componentes de la velocidad
vx=1.17 m/s
vy=14.14 m/s
Componentes tangencial y normal de la aceleración
at= 9.80 m/s2
an= 2.82 m/s2
Componentes de la velocidad
vx=6.83 m/s
vy=-14.14 m/s
Componentes tangencial y normal de la aceleración
at= 9.87 m/s2
an= 2.55 m/s2
 |
|
Movimiento uniformemente acelerado a lo largo del eje X
ax=2
vx=2t
x=2t2/2
Movimiento uniformemente acelerado a lo largo del eje Y (movimiento de caída de los cuerpos)
ay=-10
vy=20+(-10)t
y=20t+(-10)t2/2
El punto de impacto tiene de coordenadas x desconocida e y=-50 m.
Dado y se obtiene el valor de t y luego el valor de x.
y=-50 m
t=1.74 s
x=3.03 m
La altura máxima se obtiene cuando la velocidad vertical es cero
vy=0 m/s
t=2 s
y=20 m
La altura desde el suelo es 20+50=70 m
El móvil se encuentra en dos instantes a 60 m de altura sobre el suelo (10 sobre el origen), ya que su trayectoria corta en dos puntos a la recta horizontal y=10 m. La ecuación de segundo grado da dos raíces
10=20t+(-10)t2/2
t1=0.59 s y t2=3.41 s.
Componentes de la velocidad
vx=1.17 m/s
vy=14.14 m/s
Componentes tangencial y normal de la aceleración véase la figura
ax=2 m/s2
ay=-10 m/s2
![]()
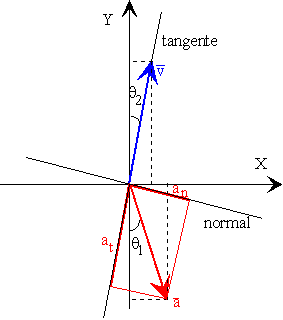 |
Los ángulos se hallan en la figura
Las componentes de la aceleración referidas a los nuevos ejes son (véase la figura) at=a cos(q1+q2)=9.80
m/s2 |
Componentes de la velocidad
vx=6.83 m/s
vy=-14.14 m/s
La componente vy de la velocidad tiene el mismo valor pero sentido contrario
Componentes tangencial y normal de la aceleración
ax=2 m/s2
ay=-10 m/s2
![]()
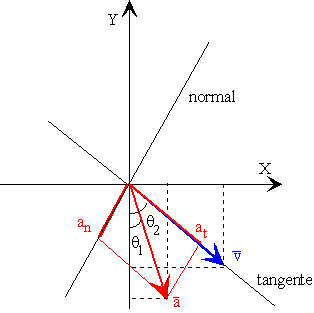 |
Los ángulos se hallan en la figura
Las componentes de la aceleración referidas a los nuevos ejes son (véase la figura) at=a cos(q2-q1)=9.87
m/s2 |