1.-Una partícula se mueve a lo largo del eje X, de manera que su posición en cualquier instante t está dada por x=5 t²+1, donde x se expresa en metros y t en segundos.

Calcular su velocidad promedio en el intervalo de tiempo entre:

• 2 y 3 s.
• 2 y 2.1 s.
• 2 y 2.01 s.
• 2 y 2.001 s.
• 2 y 2.0001 s.
• Calcula la velocidad en el instante t=2 s.

• Hallar la velocidad media del móvil entre el instante t y el instante t+Dt
• Hallar la velocidad en el instante t en el límite cuando Dt tiende a cero.
• Hallar la derivada x con respecto del tiempo.

2.-Un automóvil parte del reposo y se mueve con una aceleración de 4 m/s², y viaja durante 4 s. Durante los próximos 10 s, se mueve con movimiento uniforme. Se aplican los frenos y el automóvil desacelera a razón de 8 m/s² hasta que se detiene.

• Calcular la posición del móvil al final de cada intervalo y su posición cuando se detiene.
• Hacer un gráfico de la velocidad en función del tiempo.
• Mostrar que el área comprendida entre la curva y el eje del tiempo mide el desplazamiento total del automóvil.

3.-Un cuerpo se mueve a lo largo de una línea recta de acuerdo con la ley x=2t³-4t²+5 m. Hallar

• La velocidad
• La aceleración del móvil en función del tiempo.

4.-Un cuerpo se mueve a lo largo de una línea recta de acuerdo a la ley v=t³-4t² +5 m/s. Si en el instante t=2 s. está situado a 4 m del origen.

• Calcular la aceleración del móvil.
• La posición del móvil en cualquier instante.

5.-La aceleración de un cuerpo que se mueve a lo largo de una línea recta viene dada por la expresión. a=4-t² m/s². Sabiendo que en el instante t=3 s, la velocidad del móvil vale 2 m/s y se encuentra en la posición x=9 m.

• La expresión de la velocidad del móvil en cualquier instante
• La expresión de la posición del móvil en función del tiempo.

6.-Un objeto se lanza verticalmente con una velocidad de 60 m/s. (tomar g=10 m/s²)

• Calcular su altura y velocidad en los instantes t = 2, 4, 6, 8, 10, 12 s después del lanzamiento.
• ¿Qué altura máxima alcanza?
• ¿Cuánto tiempo tarda en regresar al suelo?

7.-Se lanza un cuerpo hacia arriba, en dirección vertical, con velocidad inicial de 98 m/s desde el techo de un edificio de 100 m de altura. Tomar g=9.8 m/s². Hallar:

• La máxima altura que alcanza el cuerpo medida desde el suelo
• El tiempo que transcurre hasta que llega al suelo.
• La velocidad al llegar al suelo

8.-Un automóvil describe una curva plana tal que sus coordenadas rectangulares, en función del tiempo están dadas por las expresiones: x=2t³-3t², y=t²-2t+1 m. Calcular:

• Las componentes de la velocidad en cualquier instante.
• Las componentes de la aceleración en cualquier instante.

9.-Un punto se mueve en el plano de tal forma que las componentes rectangulares de la velocidad en función del tiempo vienen dadas por las expresiones: v_x=4t³+4t, v_y=4t m/s. Si en el instante t=0 s, el móvil se encontraba en la posición x=1, y=2 m. Calcular:

• Las componentes de la aceleración en cualquier instante
• Las coordenadas x e y , del móvil, en función del tiempo.
• Sus valores para el instante t=1 s.

10.-Se lanza una pelota verticalmente hacia arriba con una velocidad de 20 m/s desde la azotea de un edificio de 50 m de altura. La pelota además es empujada por el viento, produciendo un movimiento horizontal con una aceleración de 2 m/s². Calcular:

• La distancia horizontal entre el punto de lanzamiento y de impacto
• La altura máxima
• El valor de las componentes tangencial y normal de la aceleración cuando la pelota se encuentra a 60 m de altura sobre el suelo.

11.-Un proyectil es disparado con una velocidad de 600 m/s, haciendo un ángulo de 60º con la horizontal. Calcular:

• La ecuación de la trayectoria, ¿Qué representa?.
• El alcance horizontal.
• La altura máxima.

12.-Se dispara un proyectil desde lo alto de una colina de 300 m de altura, haciendo un ángulo de 30º por debajo de la horizontal.

• Determinar la velocidad de disparo para que el proyectil impacte sobre un blanco situado a una distancia horizontal de 119 m, medida a partir de la base de la colina.

13.-Una partícula se está moviendo en una circunferencia, su velocidad angular en función del tiempo está dada por la expresión w=3t²-2t+2 rad/s. Sabiendo que en el instante t=0 s. el móvil se encontraba en el origen q=0. Calcular:

• La expresión de la aceleración angular en función del tiempo.
• La expresión de la posición angular en función del tiempo.
• Los valores de las magnitudes angulares en el instante t= 2 s.

14.-Una rueda de radio 10 cm está girando con una velocidad angular de 120 r.p.m., se aplican los frenos y se detiene en 4 s. Calcular:

• La aceleración angular (supuesta constante la fuerza de frenado).
• El ángulo girado a los 4 s.

Calcular 1 s. después de aplicar los frenos:

• La velocidad angular, la velocidad (lineal) de un punto de la periferia de la rueda.
• La aceleración tangencial, la aceleración normal, la aceleración resultante y el ángulo que forma con la dirección radial.

15.-Dos móviles describen una trayectoria circular en el mismo sentido. El primer móvil parte del origen, inicialmente en reposo, con aceleración angular constante de 2 rad/s²; el segundo móvil parte de la posición p/2 rad, y está animado de un movimiento uniforme con velocidad constante de 120 r.p.m.

• Determinar el instante y la posición de encuentro por primera vez de ambos móviles.

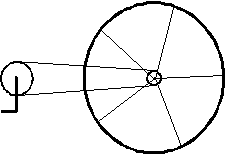16.-El plato de una bicicleta tiene 35 cm de radio y está unido mediante una cadena a un piñón de 7 cm de radio, que mueve una rueda de 75 cm de radio. Si la velocidad angular constante del plato es de 2 rad/s. Calcular: La velocidad angular del piñón y la velocidad (lineal) de un diente del piñón. La velocidad de un punto de la periferia de la rueda.

17.-Dos trenes A y B se desplazan en vías rectilíneas paralelas a 70 y 90 km/h respectivamente. Calcular la velocidad relativa de B respecto de A:

Cuando se mueven en el mismo sentido.

• Cuando se mueven en sentido contrario

18.-Un río fluye hacia el norte con velocidad de 3 km/h. Un bote se dirige al Este con velocidad relativa al agua de 4 km/h.

• Calcular la velocidad del bote respecto de tierra.
• Si el río tiene 1 km de anchura, calcular el tiempo necesario para cruzarlo.
• ¿Cuál es la desviación hacia el norte del bote cuando llega a la otra orilla del río?

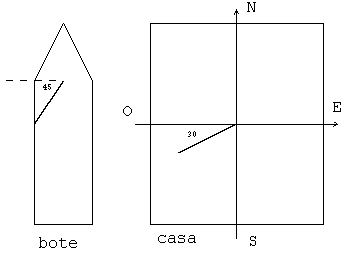19.-Una bandera situada en el mástil de un bote flamea haciendo un ángulo de 45º como se muestra en la figura. Pero la bandera situada en una casa a la orilla flamea haciendo un ángulo de 30º. Si la velocidad del bote es de 10 km/h hacia el norte. Identificar y dibujar con origen común los vectores: velocidad del viento (respecto de tierra), velocidad del bote (respecto de tierra), velocidad del viento (respecto del bote). Relacionar los tres vectores y calcular la velocidad del viento.

20.-Un avión se mueve en vuelo horizontal a una altura h sobre el suelo y con velocidad v constante. Cuando pasa justamente por encima de un observador O, el piloto del avión suelta un paquete.

• Escribir las ecuaciones del movimiento del paquete desde el punto de vista del observador O, y desde el punto de vista del piloto del avión.
• ¿Cuál es la trayectoria del paquete para el observador O, y para el piloto?