 |
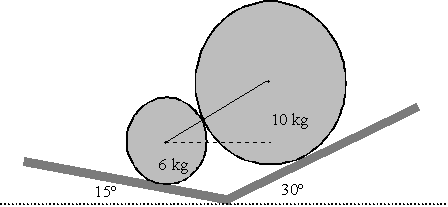
Dos cilindros macizos y homogéneos de pesos 6 y 10 kg se
apoyan sin rozamiento sobre los planos inclinados de la figura. Calcular:
|
El ángulo que forma con la horizontal la línea que une los centros de los dos cilindros vale 59.3º
La reacción del plano inclinado izquierdo es N=11.32 kp
La reacción del plano inclinado derecho es N'=5.86 kp
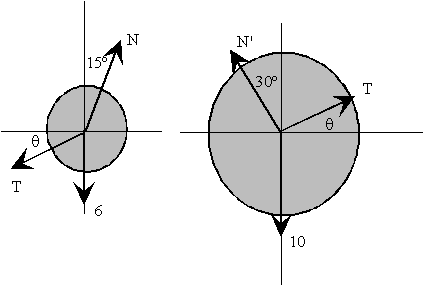 |
Equilibrio de la esfera de la izquierda T senq+6=N cos15º T cosq=N sen15º Equilibrio de la esfera de la derecha T cosq=N' sen30º T senq+N' cos30º=10 |
T es la fuerza que ejerce una esfera sobre la otra, que tiene la dirección de la recta que une los centros de las esferas. De acuerdo con la tercera ley de Newton, la fuerza que ejerce la primera esfera sobre la segunda es igual y de sentido contrario a la que ejerce la segunda sobre la primera.
Resolviendo el sistema de cuatro ecuaciones con cuatro incógnitas obtenemos
q=59.3
ºN=11.32 kp
N'=5.86 kp
T=5.73 kp