 |
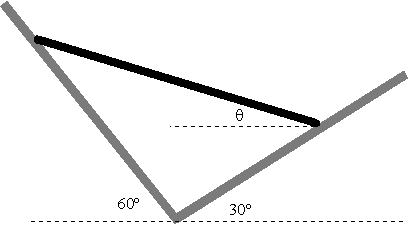
Una varilla de 6 kg y 0.8 m de longitud está apoyada sobre
un ángulo recto liso, como se muestra en la figura. Calcular :
|
El ángulo de equilibrio que forma la varilla con la horizontal vale q=30º
La reacción del plano izquierdo es F1=3 kp
La reacción del plano inclinado derecho es ![]()
Para que un sólido rígido esté en equilibrio se tienen que cumplir dos condiciones
Una vez dibujadas las fuerzas sobre la barra se sustituyen las fuerzas F1 y F2 pos sus componentes rectangulares
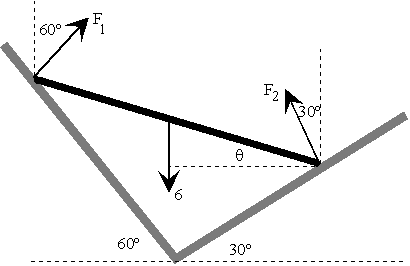 |
La resultante es cero F1 cos60º+F2 sen30º=6 F1 sen60º=F2 sen30º Momentos respecto del apoyo izquierdo -6*0.4*cosq+F2*0.8*sen(60-q)=0 |
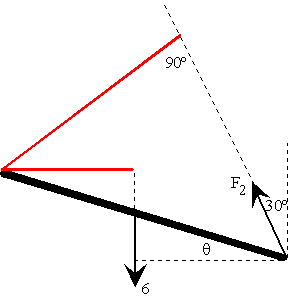 |
Para calcular el momento de las fuerzas F2 y
del peso de la barra respecto del extremo izquierdo de la misma, hay que dibujar el brazo
de dichas fuerzas, que se muestra en la figura de color rojo. El brazo de la fuerza F2 vale 0.8*sen(60-q). El brazo del peso de la barra vale 0.4*cosq. |
De las dos primeras ecuaciones del equilibrio de la barra obtenemos F1 y F2.
F1=3 kp
![]()
Para hallar el ángulo en la tercera ecuación hay que aplicar la fórmula del seno de una diferencia de dos ángulos
sen(a-b)=sena*cosb-senb*cosa
El resultado es q=30º