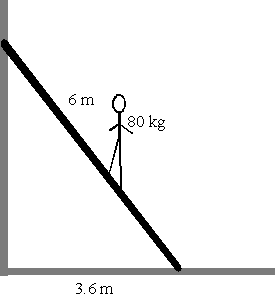 |
Una escalera, de masa 40 kg y 6 m de longitud, está apoyada
sobre una pared lisa vertical y sobre un suelo horizontal rugoso (m=0.4).
Calcular:
|
La fuerza de rozamiento cuando el hombre se encuentra a 3 m es Fr=45 kp.
La longitud máxima a lo largo de la escalera a la que puede ascender, antes de que comience a deslizar es x=3.3 m
En este problema hemos de tener en cuenta que la fuerza de rozamiento que actúa sobre un cuerpo apoyado en un plano es en general, una magnitud desconocida. Solamente podemos expresarla mediante una fórmula cuando el cuerpo está a punto de deslizar o está deslizando.
Cuando el cuerpo está a punto de deslizar, la fuerza de rozamiento vale Fr=meN, donde N es la reacción del plano a lo largo del que desliza el cuerpo, y me es el coeficiente estático de rozamiento.
La fuerza de rozamiento es una incógnita a despejar en el sistema de ecuaciones
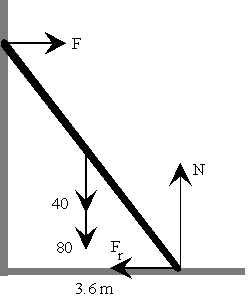 |
La resultante de las fuerzas es nula N=40+80 F=Fr La suma de los momentos respecto del extremo inferior de la escalera es cero. -F*4.8+40*1.8+80*1.8+Fr*0+N*0=0 El resultado es F=45 kp Fr=45 kp |
La fuerza de rozamiento viene dada por la fórmula Fr=meN.
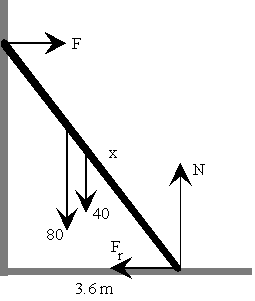 |
La resultante de las fuerzas es nula N=40+80 F=Fr La suma de los momentos respecto del extremo inferior de la escalera es cero. -F*4.8+40*1.8+80*x*0.6+Fr*0+N*0=0 El extremo inferior de la escalera está apunto de deslizar Fr=0.4*N El resultado Fr=48 kp y x=3.3 m |
Comparando el primer resultado con el segundo, vemos que en el primer caso la escalera no desliza por que la fuerza horizontal que actúa sobre el extremo inferior de la escalera y que impide que deslice vale 45 kp y es inferior al valor máximo Fr=0.4*N =48 kp.
Podemos considerar el rozamiento como una cuerda imaginaria que sujeta el extremo inferior de la escalera cuya tensión es desconocida, pero que se rompe cuando alcanza la tensión máxima meN.