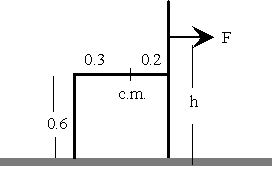
 |
Queremos arrastrar una silla a velocidad constante sobre el suelo
horizontal, siendo el coeficiente dinámico de rozamiento entre las patas y el suelo 0.3.
La silla pesa 25 kg.
|
La fuerza horizontal F=7.5 kp
Las reacciones en la pata delantera es N1=1 kp
La reacción en pata trasera es N2=24 kp.
La altura máxima a la que se puede aplicar la fuerza F es h=2/3 m, caundo la silla está a punto de volcar.
Cuando el cuerpo está deslizando la fuerza de rozamiento se puede expresar mediante una fórmula Fr=mdN, donde md es el coeficiente dinámico de rozamiento.
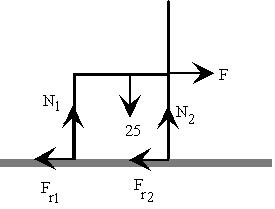 |
La resultante de las fuerzas es cero N1+N2=25 F=Fr1+Fr2 Como la silla está deslizando Fr1=0.3 N1 Fr2=0.3 N2
|
La suma de los momentos respecto al extremo inferior de la pata izquierda es cero.
-F*0.6-25*0.3+N2*0.5=0
De las dos primeras ecuaciones despejamos N1=1 kp y N2=24 kp.
De ecuación de los momentos despejamos F=7.5 kp.
Cuando la silla va a volcar
Cuando la silla va a volcar, la pata izquierda ya no toca el suelo, por tanto N1=0 y Fr1=0.
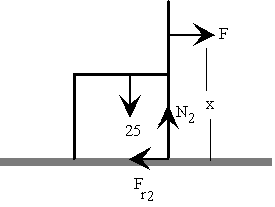 |
La resultante de las fuerzas es cero N2=25 F=Fr2 Como la silla está deslizando Fr2=0.3 N2
|
La suma de los momentos respecto al extremo inferior de la pata derecha es cero
-F*x+25*0.2=0
De las dos primeras ecuaciones obtenemos F=7.5 kp
De la ecuación de los momentos obtenemos x=2/3 m.