 |
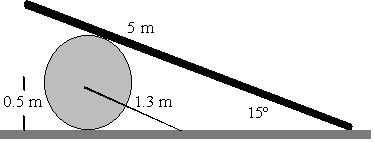
En el problema esquematizado en la figura, la barra tiene una longitud de
5 m y pesa 20 kg, el cilindro tiene un peso de 30 kg y un radio de 0.5 m. Suponer que no
hay rozamiento entre la barra y el cilindro, y que el coeficiente est tico de
rozamiento entre el extremo derecho de la barra y el plano horizontal es 0.3. La esfera
está sujeta, a su vez, por una cuerda de 1.3 m de longitud.
|
La fuerza de rozamiento vale Fr=3.3 kp
La tensión de la cuerda T=3.6 kp
La barra deslizará
En este problema hemos de tener en cuenta que la fuerza de rozamiento que actúa sobre un cuerpo apoyado en un plano es en general, una magnitud desconocida. Solamente podemos expresarla mediante una fórmula cuando el cuerpo está a punto de deslizar o está deslizando.
Cuando el cuerpo está a punto de deslizar, la fuerza de rozamiento tiene el valor máximo Fr=meN, donde N es la reacción del plano a lo largo del que desliza el cuerpo, y me es el coeficiente estático de rozamiento.
Equilibrio de la barra
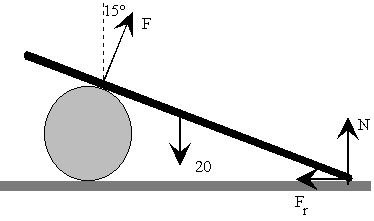 |
La resultante de las fuerzas es cero F cos15º+N=20 F sen15º=Fr La suma de los momentos respecto al extremo derecho de la barra es cero N*0+Fr*0-F*x+20*2.5*cos15=0 |
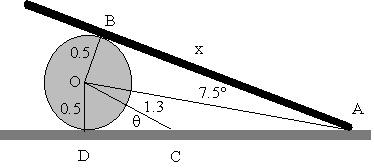 |
El valor de x (brazo de F) y el ángulo q se obtienen de la figura
|
De la ecuación de los momentos obtenemos el valor de F, fuerza que ejerce el cilindro sobre la barra F=12.7 kp.
Y de las dos primeras ecuaciones despejamos Fr=3.3 kp y N=7.7 kp.
Equilibrio del cilindro
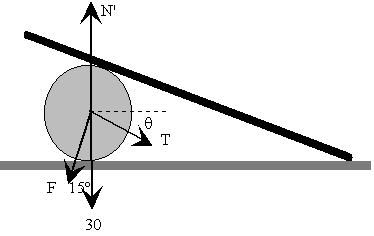 |
Todas las fuerzas que actúan sobre el cilindro pasan por su
centro. La resultante es cero. N'=T senq+F cos15º+30 F sen15º=T cosq Se obtiene T=3.6 kp y N'=43.6 kp |
El máximo valor de la fuerza de rozamiento es 0.3 N=2.31 kp. El valor calculado es Fr=3.3 kp. Luego la barra NO puede estar en equilibrio en esta posición.