 |
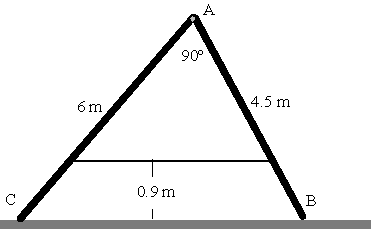
Dos escaleras CA y DA de 40 kg y 30 kg, respectivamente, se apoyan sobre
un suelo liso y se articulan en el vértice A, están sujetas por una cuerda paralela al
suelo situada a 0.9 m del mismo. Las escaleras forman entre sí un ángulo recto.
Calcular:
|
La reacción en el apoyo C es NC=32.6 kp, y la reacción en el apoyo B es NB=37.4 kp
La tensión de la cuerda es T=22.4 kp
Las componentes horizontal y vertical de la fuerza que una escalera ejerce sobre la otra a través de la articulación A son Fx=22.4 kp y Fy=7.4 kp.
Tenemos una articulación común A para las dos escaleras. De acuerdo con la tercera ley de Newton la fuerza que ejerce la escalera izquierda sobre la escalera derecha debe ser igual y de sentido contrario a la que ejerce la escalera derecha sobre la izquierda a través de la articulación común.
Equilibrio de la escalera izquierda
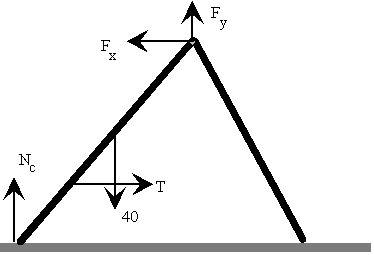 |
La resultante de las fuerzas es cero Fy+NC=40 Fx=T La suma de los momentos de las fuerzas respecto el punto A es cero -NC*6*cosq1+40*3*cosq1+T*(6*senq1-0.9)=0 |
Equilibrio de la escalera derecha
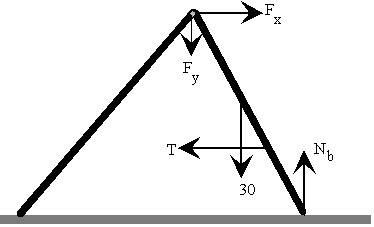 |
La resultante de las fuerzas es cero Fy+30=NB Fx=T La suma de los momentos de las fuerzas respecto el punto A es cero NB*4.5*cosq2-30*2.25*cosq2+ T*(4.5*senq1-0.9)=0 |
Geometría de la escalera de tijera
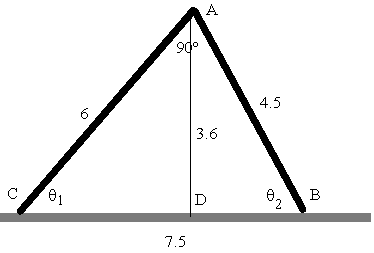 |
Los ángulos q1 y
q2 se obtienen a partir de la figura La hipotenusa CB vale 7.5 cosq1=0.8, senq1=0.6 cosq2=0.6, senq2=0.8 por ser q1 y q2 ángulos complementarios |
Tenemos un sistema de 5 ecuaciones con cinco incógnitas (una de las ecuaciones se repite). La solución del sistema es
NC=32.6 kp, y NB=37.4 kp
T=22.4 kp
Fx=22.4 kp y Fy=7.4 kp.