|
Se denomina momento de una fuerza respecto de un punto, al producto vectorial del
vector posición r de la fuerza por el vector fuerza F.
M=r´F
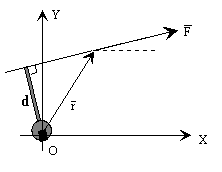 |
La analogía de la llave y el tornillo, nos ayuda a entender el
significado físico de la magnitud momento, y a determinar correctamente el módulo, la
dirección y el sentido del momento de una fuerza:
- El módulo es el producto de la fuerza por su brazo (la distancia desde el punto O a la
recta de dirección de la fuerza). M=Fd
- La dirección perpendicular al plano que contiene la fuerza y el punto, la que marca el
eje del tornillo.
- El sentido viene determinado por el avance del tornillo cuando hacemos girar a la llave.
|
Ejemplo
Supongamos que tenemos tres llaves que actúan sobre tres tornillos en la forma
indicada por las figuras. Se aplica una fuerza F en el extremo de la llave. Es
fácil contestar a las siguientes preguntas:
- ¿En qué situaciones se introduce el tornillo?
- ¿En que situaciones se saca el tornillo?
- ¿Cuáles producen el mismo resultado o son equivalentes?.
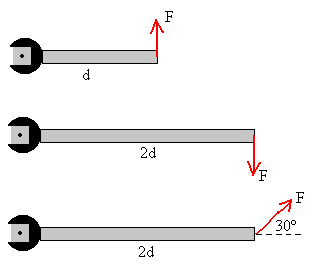 |
En la primera figura, el tornillo avanza en una dirección perpendicular
al plano de la página, y hacia el lector. El módulo del momento es F·d. En la
segunda figura, el tornillo avanza en una dirección perpendicular al plano de la página,
y hacia dentro (sentido contrario al anterior). El módulo del momento es F·2d.
Con una llave más larga estamos en una situación más favorable que disponiendo de una
llave más corta.
En la tercera figura, el tornillo avanza en una dirección perpendicular al plano de la
página, y hacia el lector. El módulo del momento es F·sen30·2d=F·d. Esta
situación es equivalente a la primera. |
- Un momento se considera positivo si el tornillo sale, avanza hacia el lector, la llave
gira en sentido contrario a las agujas del reloj.
- Un momento se considera negativo si el tornillo entra, la llave gira en el sentido de
las agujas del reloj.
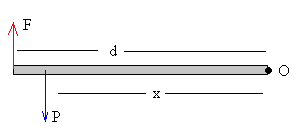 |
Supongamos una barra de masa despreciable, que está sujeta por su extremo
O. Si colocamos un peso P a una distancia x del origen. El momento de esta
fuerza respecto del origen O es P·x.
Para que la barra está en equilibrio la fuerza F deberá ser tal que el momento
total sea nulo. -F·d+P·x=0, de modo que F=P·x/d. |
Tenemos una barra de 50 cm de longitud, que dispone de ganchos situados en las
divisiones 0, 5, 10, ... 50 cm. Un extremo de la barra (el origen) está sujeto y del otro
extremo cuelga de un dinamómetro. El dinamómetro se ha ajustado de modo que cuando no
cuelga ninguna pesa en la barra éste marque cero.
Se pulsa el botón titulado Nuevo aparecen pesas de distintos colores de 10 g,
25 g y 50 g . Con el puntero del ratón arrastramos una de las tres pesas y la colgamos de
la barra en alguna de las posiciones marcas. Disponemos solamente dos pesas de cada tipo.
Cogemos otra pesa y la colgamos de la barra y así sucesivamente, hasta un máximo de
seis pesas (dos de cada tipo).Podemos colgar más de una pesa en la misma posición, una
debajo de la otra.
El dinamómetro nos muestra la fuerza F que ejerce en el extremo izquierdo de la
barra, para mantenerla horizontal y en equilibrio. La fuerza viene expresada en gramos que
podemos convertir a newtons.
1gramo-fuerza=0.001·9.8=0.0098 N» 0.01 N
- Primero, probamos con una sola pesa colocándola en varias posiciones y anotamos la
fuerza que ejerce el dinamómetro.
Se pulsa el botón titulado Nuevo, se coloca una pesa colgada de un gancho, se
apunta el valor de la fuerza F que marca el dinamómetro. Se pulsa el botón Nuevo,
se elige la misma pesa y se coloca en otro gancho y así sucesivamente.
Fijarse que las pesas situadas en el origen no ejercen momento alguno. Y aquellas que
están situadas al otro extremo de la barra ejercen un momento máximo.
- Después, probamos con varias pesas en distintas posiciones coincidentes o no.
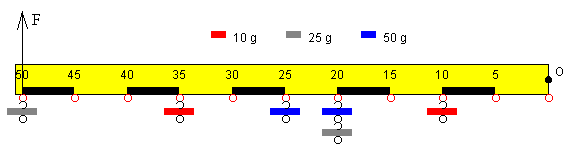
Supongamos que hemos colgado las seis pesas disponibles en las posiciones que se
indican en la figura
| Pesa (g) |
Brazos (cm) |
Momento |
| 10 |
35 |
10 |
450 |
| 25 |
50 |
20 |
1750 |
| 50 |
25 |
20 |
2250 |
| Total |
4450 |
El momento total es igual al momento de la fuerza que ejerce el dinamómetro, para que
el sistema esté en equilibrio.
4450-F·50=0, por lo que F=89 gramos-fuerza=0.87 N.
|