| Una espira cuadrada de lado a, se mueve hacia una región
rectangular de lado 2a en la que existe un campo magnético constante perpendicular
al plano de la espira. Determinar la fem y el sentido de la corriente inducida en las
siguientes situaciones
- Cuando la espira está entrando en dicha región
- Cuando está completamente introducida en la región en la que hay campo
- Cuando empieza a salir de dicha región.
Este ejemplo es similar en su discusión a la varilla
que se mueve en un campo magnético uniforme
Vamos a obtener el valor de la fem y el sentido de la corriente inducida por dos
procedimientos:
- La ley de Faraday
para calcular la fem y la ley de Lenz para determinar el sentido de la corriente inducida
- A partir de la fuerza sobre los portadores de carga positiva que se mueven con la
varilla en el seno de un campo magnético uniforme
La ley de Faraday
Primera etapa
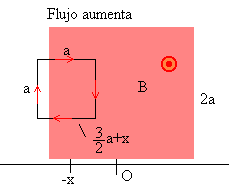 |
Supongamos que el campo magnético B es constante y es
perpendicular al plano determinado por la espira. El flujo del campo magnético a través
de la superficie de la espira que se ha introducido en la región en la que existe el
campo magnético es 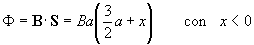
|
De acuerdo a la ley
de Faraday, la fem inducida es
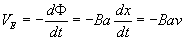
La derivada de x respecto del tiempo es la velocidad constante v>0 de
la espira.
- Sentido de la corriente inducida
El flujo aumenta, al aumentar el área de la parte de la espira introducida en el campo
magnético, el sentido de la corriente inducida es el de las agujas del reloj.
Si la resistencia de la espira es R, la intensidad de la corriente inducida es i=VE/R=vBa/R.
Segunda etapa
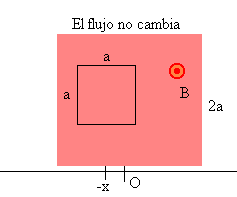 |
La espira se halla completamente introducida en la región en la que
existe campo magnético uniforme. 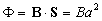
El flujo es constante, la fem es nula
VE=0 |
Tercera etapa
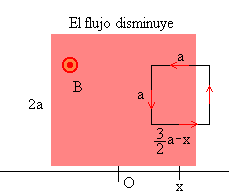 |
La espira empieza a salir del la región en la que existe campo magnético El
flujo del campo magnético a través de la superficie de la espira que está introducida
en dicho campo es
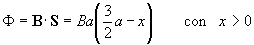
|
De acuerdo a la ley de Faraday, la fem inducida es
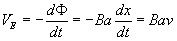
La derivada de x respecto del tiempo es la velocidad constante v>0 de
la espira.
- Sentido de la corriente inducida
El flujo disminuye, al disminuir el área de la parte de la espira introducida en el
campo magnético, el sentido de la corriente inducida es el contrario al de las agujas del
reloj.
Explicación en términos de las fuerzas sobre los portadores de cargas
Primera etapa
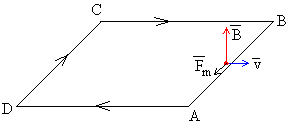 |
Tomemos un portador de carga positivo en del lado AB de la espira que se
ha introducido en el campo magnético. Este portador de carga experimenta una fuerza en el
sentido de B hacia A. Los portadores de carga son
"bombeados" de B hacia A por la acción del campo magnético (de un
potencial menor a uno mayor). Los portadores de carga que llegan a A "descienden
espontáneamente" (hacia un potencial menor) hacia B por el camino A D C y B. |
Las fuerzas sobre los portadores de carga situados en los lados paralelos al
movimiento, como puede comprobar el lector, no afectan a la corriente inducida.
Segunda etapa
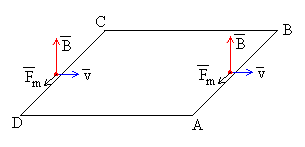 |
Tomemos un portador de carga positivo en del lado AB de la espira que se
ha introducido en el campo magnético. Este portador de carga experimenta una fuerza en el
sentido de B hacia A. Tomemos ahora un portador de carga positivo en el lado CD. Las
fuerzas sobre los portadores de carga tienen el mismo sentido. Ambas fuerzas
"bombean" cargas hacia el mismo lado, por lo que el potencial de A es el mismo
que el de D, y el potencial de B es el mismo que el de C. No se establece por tanto,
corriente en el circuito. |
Tercera etapa
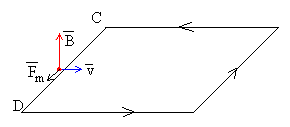 |
Tomemos un portador de carga positivo en del lado CD de la espira que
está introducido en el campo magnético. Este portador de carga experimenta una fuerza en
el sentido de C hacia D. Los portadores de carga son "bombeados" de C hacia D
por la acción del campo magnético de un potencial menor a uno mayor. Los portadores de
carga que llegan a D "descienden espontáneamente" hacia C por el camino D A B y
C. |
Como en el caso de una varilla que se mueve en un campo magnético uniforme. Es
necesario ejercer una fuerza Fa sobre la varilla para que se mueva con
velocidad constante. Esta fuerza es igual y de sentido contrario a la fuerza
que ejerce el campo magnético sobre la porción de corriente rectilínea de longitud L
por la que circula una corriente i.
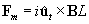
El vector unitario ut que señala el sentido de la corriente y
el campo B son mutuamente perpendiculares, la longitud del conductor es a, por
lo que el módulo de la fuerza magnética es Fm=iBa
Primera etapa
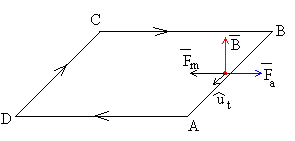 |
Cuando la espira penetra en el campo magnético, sobre el lado AB el campo
magnético ejerce una fuerza Fm=iBa, dirigida hacia la izquierda (de
sentido contrario al movimiento). Para mantener la velocidad constante tendremos que
aplicar una fuerza igual y de sentido contrario Fa dirigida hacia la
derecha. |
Segunda etapa
Como no hay corriente inducida, la fuerza magnética sobre la espira es cero, y en
ausencia de rozamiento no es necesario aplicar ninguna fuerza.
Tercera etapa
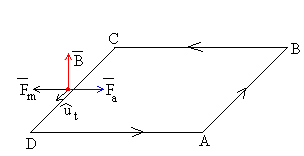 |
El lado CD está en el interior del campo magnético uniforme. La fuerza
que ejerce el campo magnético sobre esta porción de conductor es Fm=iBa,
y esta dirigida hacia la izquierda (en sentido contrario al del movimiento). Para mantener
la velocidad constante tendremos que aplicar una fuerza igual y de sentido contrario Fa
dirigida hacia la derecha. |
Como en el caso de la varilla que
se desplaza en un campo magnético uniforme, se puede demostrar de forma análoga que
la energía por unidad de tiempo suministrada por la fuerza Fa, se
disipa en la resistencia de la espira por efecto Joule.
El applet nos permite estudiar el movimiento de una espira cuando entra y sale de una
región en la que existe un campo magnético uniforme perpendicular al plano de la espira.
Introducimos
- El campo magnético (en gauss), que es un número positivo o negativo. La
discusión anterior se ha basado en el primer caso, y se deja al lector describir el
segundo.
- La velocidad de la varilla (en cm/s), un número positivo menor que 10.
- Finalmente, podemos elegir el tipo de vista del fenómeno (en el espacio, o en el plano
de la espira) activando o desactivando la casilla titulada Vista en el plano horizontal.
Se pulsa el botón titulado Empieza, y la espira se mueve hacia la derecha con
velocidad constante. Se puede detener la marcha del "experimento" en cualquier
momento pulsando en el botón titulado Pausa. Se reanuda, volviendo a pulsar el
mismo botón titulado ahora Continua. Se puede ver la evolución de la
"experiencia" paso a paso pulsando el botón titulado Paso.
Con la casilla Vista en plano horizontal desactivada, observamos el sentido de
la corriente inducida por medio del movimiento de pequeños círculos de color rojo que
representan a los portadores de carga positiva.
Se dibujan las fuerzas sobre los portadores de carga positiva situados en lados
perpendiculares a la dirección del movimiento.
Con la casilla Vista en plano horizontal activada vemos la
"experiencia" tal como la dibujamos en el papel. En la parte inferior del
applet, se representa la fem en función de la posición del centro de la espira medida
desde un origen situado en el centro de la región en la que existe campo magnético.
El cálculo de fem nos ha proporcionado el mismo valor que en el caso de la varilla que
se mueve en un campo magnético uniforme, VE=vBa
Ejemplo
- Sea el valor del campo magnético B, 40 gauss= 40·10-4 T
- La velocidad v=5 cm/s=0.05 m/s
- La dimensión de la espira a=10 cm =0.1 m está fijada en el programa
El valor de la fem inducida es VE=2·10-5 voltios
Se recomienda al lector dibujar sobre un papel la espira y la región en la que existe
un campo magnético uniforme perpendicular al plano de la espira, en las tres situaciones
señaladas:
- Cuando la espira está entrando en dicha región
- Cuando está completamente introducida en la región en la que hay campo
- Cuando empieza a salir de dicha región.
- Razonar si el flujo aumenta o disminuye
- Aplicar la ley de Lenz y dibujar el sentido de la corriente inducida
- Compararlos con los que proporciona el programa interactivo.
|